Question

What is the dimension of Reynolds number?
A. It is dimensionless
B. N/m
C. Pascal
D. Tesla

Answer 1

Hint: Reynolds number refers to the flow of a fluid in a pipe. The approximate range of Reynolds number can give information regarding the kind of flow in the pipe. The formula of the Reynolds number ${{N}_{\operatorname{Re}}}$ is, ${{N}_{\operatorname{Re}}}=\dfrac{\rho vd}{\mu }$

Complete answer:
Let’s start by the definition of Reynolds number. In simple words, the Reynolds number is the ratio of the inertial forces acting on a fluid flowing through a closed surface such as a pipe to the viscous forces acting on it. Since, the Reynolds number is just a ratio of 2 forces, hence it is a dimensionless quantity.
The formula of the Reynolds number ${{N}_{\operatorname{Re}}}$is, ${{N}_{\operatorname{Re}}}=\dfrac{\rho vd}{\mu }$
Where:
$\rho $ is the density of the fluid. Its dimensional formula is: \[\left[ \rho \right]=\left[ {{M}^{1}}{{L}^{-3}}{{T}^{0}} \right]\].
$v$ is the velocity of the fluid, with which it is flowing through the pipe. Its dimensional formula is: \[\left[ v \right]=\left[ {{M}^{0}}{{L}^{1}}{{T}^{-1}} \right]\].
$d$ is the diameter of the pipe. Its dimensional formula is: \[\left[ L \right]=\left[ {{M}^{0}}{{L}^{1}}{{T}^{0}} \right]\].
$\mu $ is the viscosity of the fluid. Viscosity of a fluid is given by the distance between the layers of the fluid times the force divided by the area of the layer and the velocity of the layer. Hence, Its dimensional formula is: \[\mu =\dfrac{l\times F}{A\times v}\Rightarrow \left[ \mu \right]=\dfrac{\left[ {{M}^{0}}{{L}^{1}}{{T}^{0}} \right]\times \left[ {{M}^{1}}{{L}^{1}}{{T}^{-2}} \right]}{\left[ {{M}^{0}}{{L}^{2}}{{T}^{0}} \right]\times \left[ {{M}^{0}}{{L}^{1}}{{T}^{-1}} \right]}\Rightarrow \left[ \mu \right]=\left[ {{M}^{1}}{{L}^{-1}}{{T}^{-1}} \right]\].

Therefore, the dimension of Reynolds number is:
$\begin{align}
  & {{N}_{\operatorname{Re}}}=\dfrac{\rho vd}{\mu }\Rightarrow \left[ {{N}_{\operatorname{Re}}} \right]=\dfrac{\left[ \rho \right]\left[ v \right]\left[ d \right]}{\left[ \mu \right]}\Rightarrow \left[ {{N}_{\operatorname{Re}}} \right]=\dfrac{\left[ {{M}^{1}}{{L}^{-3}}{{T}^{0}} \right]\times \left[ {{M}^{0}}{{L}^{1}}{{T}^{-1}} \right]\times \left[ {{M}^{0}}{{L}^{1}}{{T}^{0}} \right]}{\left[ {{M}^{1}}{{L}^{-1}}{{T}^{-1}} \right]} \\
 & \Rightarrow \left[ {{N}_{\operatorname{Re}}} \right]=\left[ {{M}^{0}}{{L}^{0}}{{T}^{0}} \right] \\
\end{align}$
The Reynolds number gives information about the flow of the fluid through a pipe. That is the pattern of the flow can be found out by calculating the Reynolds number.
The below image will help in better understanding of two specific kinds of flow of fluid.

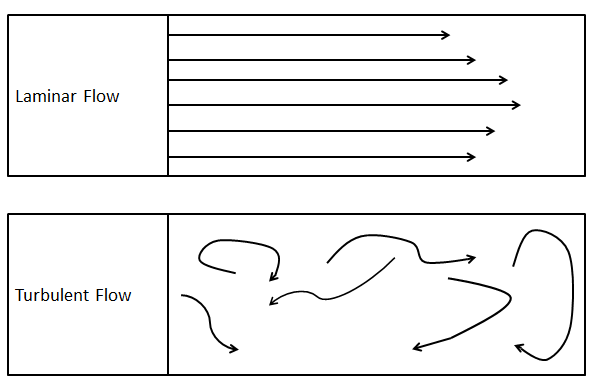
So, the correct answer is “Option A”.

Note:
The image is important in understanding what is the difference between laminar flow and turbulent flow.
$\to $Laminar flow: Also known as viscous flow, is the type of flow in which the fluid tends to flow in layers also known as laminations. For example, let’s take a transparent pipe and we’ve water flowing through it. The rate of water flow can be controlled by us. We inject a dye into the flow of water. During the laminar flow, we can see that the dye is flowing smoothly making straight lines.

$\to $Turbulent flow: In this kind of flow, the fluid makes eddies or turbulence during its flow through the pipe. Considering the same example from above, let’s give the speed of the water. Now, you can see that the water is no longer flowing smoothly, but instead the flow is disturbed. Upon injecting the dye, you’ll find that the dye is making eddies and not moving in straight lines. The main reason is due to the differences in speeds between different layers of the fluid, which causes eddies to form.