
Discuss the necessity of radius of gyration. Define it. On what factors does it depend and it does not depend? Can you locate a similarity between the centre of mass and radius of gyration? What can you infer if a uniform ring and a uniform disc have the same radius of gyration?
Answer
411.6k+ views
1 likes
Hint: The radius of gyration is occasionally used to express a body's moment of inertia about an axis. The radius of gyration can be defined as the imaginary distance from the centroid at which the cross-sectional area is believed to be centred at a point in order to achieve the same moment of inertia. The letter
Complete step by step answer:
Definition: The radius of gyration of a rotating body about an axis is defined as the distance between the axis of rotation and the point at which the full mass of the body can be assumed to be concentrated in order to produce the same moment of inertia as the body about the given axis. The moment of inertia
(I) It’s mass and
(ii) It’s mass distribution about the rotation axis.
By defining the
Physical significance: If
where
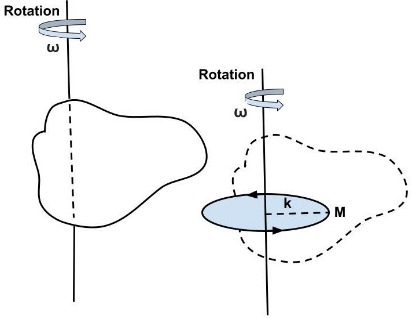
Similarly, the radius of gyration locates a point away from the axis of rotation where the total mass M can be thought to be concentrated, and the angular acceleration of that point mass about the axis of rotation obeys the relation,
where
A thin ring of radius
A thin disc of radius
Given,
Note: The radius of gyration is a measurement that is used to examine how different structural geometries would behave when compressed along an axis. It's used to anticipate buckling in compression members and beams.
Complete step by step answer:
Definition: The radius of gyration of a rotating body about an axis is defined as the distance between the axis of rotation and the point at which the full mass of the body can be assumed to be concentrated in order to produce the same moment of inertia as the body about the given axis. The moment of inertia
(I) It’s mass and
(ii) It’s mass distribution about the rotation axis.
By defining the
Physical significance: If
where
Similarly, the radius of gyration locates a point away from the axis of rotation where the total mass M can be thought to be concentrated, and the angular acceleration of that point mass about the axis of rotation obeys the relation,
where
A thin ring of radius
A thin disc of radius
Given,

Note: The radius of gyration is a measurement that is used to examine how different structural geometries would behave when compressed along an axis. It's used to anticipate buckling in compression members and beams.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




