Question

Discuss the principle and action of a Bainbridge mass spectrometer to determine the isotopic masses.

Answer 1

Hint: There are two types of fields used in Bainbridge mass spectrometer, electric and magnetic fields. Only ions having particular velocity are allowed to enter through the velocity selector. The force due to the magnetic field does not work, it only changes the direction of the moving particle.

Complete step-by-step solution:

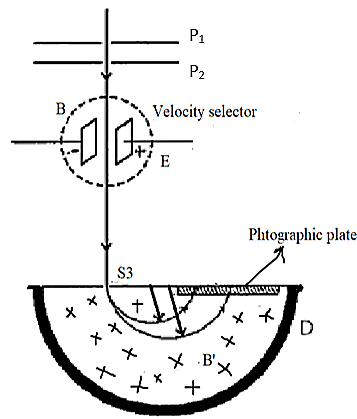
An instrument called Bainbridge mass spectrometer is used for the determination of atomic masses. If one or more electrons are removed from the atom then it has a net positive charge and it becomes a positive ion. Using two narrow slits ${{S}_{1}}$ ​and ${{S}_{2}}$, a beam of positive ions produced in a discharge tube is collimated into a fine beam. This fine beam then enters into a velocity selector. Only the ions of a particular velocity are allowed to come out from the velocity selector. The velocity selector consists of two plane parallel plates ${{P}_{1}}$ ​and${{P}_{2}}$, which produces a uniform electric field, it also has an electromagnet which produces a uniform magnetic field. These electric and magnetic fields are at right angles to each other and to the direction of the beam.
The electric field and magnetic field are so adjusted in such a way that the deflection produced by one field is nullified by the other so that the ions do not suffer any deflection within the velocity selector.
Let E be the electric field intensity, B be the magnetic induction respectively and q be the charge on the positive ion.
The force exerted by the electric field is
${{F}_{E}}=qE$
The force exerted by the magnetic field is
${{F}_{B}}=qvB$
Where $v$ is the velocity of positive ions.
We have,
${{F}_{E}}={{F}_{B}}$
$\begin{align}
  & \therefore qE=qvB \\
 & \therefore v=\dfrac{E}{B} \\
\end{align}$
The ions having this velocity are allowed to pass through the velocity selector. Then they pass through a slit ${{S}_{3}}$ and then they enter in evacuated chamber D. The positive ions having the same velocity are again influenced by another strong uniform magnetic field of induction at right angles to the plane of the paper acting inwards. These ions then move in a circular path of radius R and strike the photographic plate. The centripetal force is provided by this magnetic field. Therefore,
\[\begin{align}
  & \dfrac{m{{v}^{2}}}{R}=qv{B}' \\
 & \therefore m=\dfrac{q{B}'R}{v} \\
\end{align}\]
Using$v=\dfrac{E}{B}$, we get
$m=\dfrac{B{B}'qR}{E}$
Ions having different masses trace different semi-circular paths and produce dark lines on the plate. The distance between the opening of the chamber and the position of the dark line is equal to the diameter $2R$ from which radius R can be calculated.
By knowing $B,{B}',E\text{ and }R$, the mass of the positive ions and isotopic masses can be calculated

Note: In this method, we can distinguish the ions based on their mass as ions having different masses trace semicircles of different radii. Be careful while handling the instrument because it contains electric and magnetic fields that can harm you. Do not apply fields of very large value.