Question

Discuss the variation in $g$ with
(a). Altitude
(b). Depth

Answer 1

- Hint: Apply Shell’s theorem which states that a spherically symmetric object affects other objects gravitationally as if all of its mass were concentrated at its centre. Different points, above and inside earth are considered and variation in g is deduced.

Complete step-by-step solution -

Earth can be considered as a uniform sphere of mass M and radius R. Where the Gravitational constant is given as G. We know that on the surface of Earth acceleration due to gravity is
$g=\dfrac{GM}{{{R}^{2}}}$
We now apply shell’s theorem. Shell’s theorem states that a spherically symmetric object affects other objects gravitationally as if all of its mass were concentrated at its centre. Consider Earth as the shell.

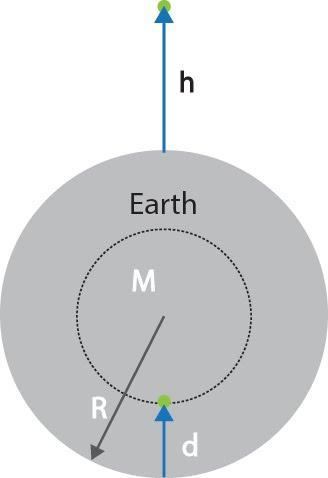
Part(a) Altitude
Let the point be taken at a height h above the earth’s surface. Applying the shell’s theorem for the figure we can write the acceleration due to gravity at that point as
$g'=\dfrac{GM}{{{r}^{2}}}=\dfrac{GM}{{{(R+h)}^{2}}}$
The relation clearly shows that with an increase in height the acceleration due to gravity decreases.

Part(b) Depth
Let the point be taken at a depth d below the earth’s surface. Applying the shell’s theorem for the figure we can observe that only the mass which lies inside the sphere of radius R-d is responsible for the acceleration due to gravity at that point.
\[\begin{align}
  & \dfrac{\text{Mass of sphere inside}}{\text{Mass of complete sphere }}=\left[ \dfrac{M'}{M} \right]={{\left[ \dfrac{R-d}{R} \right]}^{3}} \\
 & g'=\dfrac{GM'}{{{r}^{2}}}=\dfrac{GM}{{{(R-d)}^{2}}}{{\left[ \dfrac{R-d}{R} \right]}^{3}}=\dfrac{GM}{{{R}^{2}}}\left[ \dfrac{R-d}{R} \right] \\
\end{align}\]
The relation clearly shows that with an increase in depth the acceleration due to gravity decreases.

Note: Since the force due to gravity is a vector, it is possible to prove the shell’s theorem. Additionally, the theorem also states that at any point inside a hollow shell, force due to gravity becomes zero.