
Answer
108.3k+ views
Hint: Observe the type of triangle given in the question. The centroid of a triangle is a point where the medians of the triangle intersect. The circumcentre of a triangle at which all the perpendicular bisectors intersect. It can also be said that the circumcentre of a triangle is the center of the circle circumscribing it. The coordinates of the centroid of a triangle having the vertices as $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)$ are $\left( { \dfrac{{{x_1} + {x_2} + {x_3}}}{3}, \dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$ respectively.
Formula used:
1. The distance between the two points \[\left( {{x_1},{y_1}} \right)\]and \[\left( {{x_2},{y_2}} \right)\] is given by the distance formula.
\[d=\sqrt{(\mathrm{(x_2-x_1)}^2)+(\mathrm{(y_2-y_1)}^2)}\]
2. We know that the coordinates of the centroid of a triangle having the vertices as $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)$ are:
$\left( { \dfrac{{{x_1} + {x_2} + {x_3}}}{3}, \dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
Complete step by step Solution:
We know that the coordinates of the centroid of a triangle having the vertices as $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)$ are:
$\left( { \dfrac{{{x_1} + {x_2} + {x_3}}}{3}, \dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
Hence, for a triangle with vertices (6,0), (0,6), and (6,6), the coordinates of its centroid are:
$\left( { \dfrac{{6 + 0 + 6}}{3}, \dfrac{{0 + 6 + 6}}{3}} \right) = \left( {4,4} \right)$
Therefore, the coordinates of the centroid are (4,4) respectively. … (1)
Plotting the given coordinates on the coordinate plane to obtain the triangle,
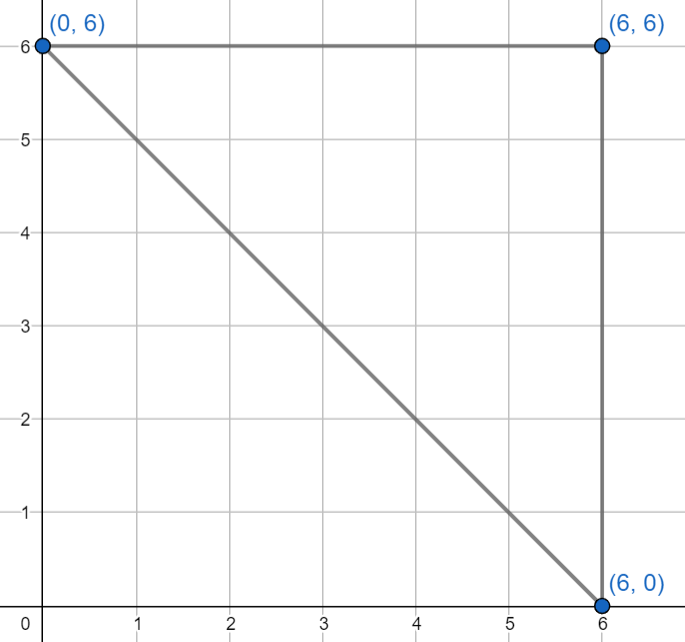
The obtained triangle is a right-angle triangle.
For a right-angle triangle, the circumcentre lies at the midpoint of the hypotenuse itself, as that is where the perpendicular bisectors meet.
Thus, for the given triangle, the circumcentre is at the midpoint point of the hypotenuse respectively.
Using the ratio formula, the coordinates of the midpoint of the hypotenuse are:
$\left( { \dfrac{{0 + 6}}{2}, \dfrac{{6 + 0}}{2}} \right) = (3,3)$
Hence, the coordinates of the circumcentre of the given triangle are (3,3) respectively.
Now, we’ll calculate the distance between the centroid and the circumcentre using the distance formula.
The distance between (4,4) and (3,3) is calculated as:
$\sqrt {{{(4 - 3)}^2} + {{(4 - 3)}^2}} = \sqrt 2 $
Hence, the distance between the centroid and the circumcentre of the given triangle is $\sqrt 2 $ units respectively.
Therefore, the correct option is B.
Note: Consider a right-angle triangle and a circle circumscribing at. As the hypotenuse subtends a right angle at the circumference of the circle circumscribing the triangle, this makes the hypotenuse a diameter of the circumcircle. Now, the center of this circle is the midpoint of its diameter, that is, the hypotenuse. Hence, the circumcentre of a right-angle triangle is at the center of its hypotenuse.
Formula used:
1. The distance between the two points \[\left( {{x_1},{y_1}} \right)\]and \[\left( {{x_2},{y_2}} \right)\] is given by the distance formula.
\[d=\sqrt{(\mathrm{(x_2-x_1)}^2)+(\mathrm{(y_2-y_1)}^2)}\]
2. We know that the coordinates of the centroid of a triangle having the vertices as $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)$ are:
$\left( { \dfrac{{{x_1} + {x_2} + {x_3}}}{3}, \dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
Complete step by step Solution:
We know that the coordinates of the centroid of a triangle having the vertices as $\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\left( {{x_3},{y_3}} \right)$ are:
$\left( { \dfrac{{{x_1} + {x_2} + {x_3}}}{3}, \dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
Hence, for a triangle with vertices (6,0), (0,6), and (6,6), the coordinates of its centroid are:
$\left( { \dfrac{{6 + 0 + 6}}{3}, \dfrac{{0 + 6 + 6}}{3}} \right) = \left( {4,4} \right)$
Therefore, the coordinates of the centroid are (4,4) respectively. … (1)
Plotting the given coordinates on the coordinate plane to obtain the triangle,

The obtained triangle is a right-angle triangle.
For a right-angle triangle, the circumcentre lies at the midpoint of the hypotenuse itself, as that is where the perpendicular bisectors meet.
Thus, for the given triangle, the circumcentre is at the midpoint point of the hypotenuse respectively.
Using the ratio formula, the coordinates of the midpoint of the hypotenuse are:
$\left( { \dfrac{{0 + 6}}{2}, \dfrac{{6 + 0}}{2}} \right) = (3,3)$
Hence, the coordinates of the circumcentre of the given triangle are (3,3) respectively.
Now, we’ll calculate the distance between the centroid and the circumcentre using the distance formula.
The distance between (4,4) and (3,3) is calculated as:
$\sqrt {{{(4 - 3)}^2} + {{(4 - 3)}^2}} = \sqrt 2 $
Hence, the distance between the centroid and the circumcentre of the given triangle is $\sqrt 2 $ units respectively.
Therefore, the correct option is B.
Note: Consider a right-angle triangle and a circle circumscribing at. As the hypotenuse subtends a right angle at the circumference of the circle circumscribing the triangle, this makes the hypotenuse a diameter of the circumcircle. Now, the center of this circle is the midpoint of its diameter, that is, the hypotenuse. Hence, the circumcentre of a right-angle triangle is at the center of its hypotenuse.
Recently Updated Pages
If x is real then the maximum and minimum values of class 10 maths JEE_Main

If one of the roots of equation x2+ax+30 is 3 and one class 10 maths JEE_Main

The HCF of two numbers is 96 and their LCM is 1296 class 10 maths JEE_Main

The height of a cone is 21 cm Find the area of the class 10 maths JEE_Main

In a family each daughter has the same number of brothers class 10 maths JEE_Main

If the vertices of a triangle are ab cc b0 and b0c class 10 maths JEE_Main

Other Pages
Electric field due to uniformly charged sphere class 12 physics JEE_Main

Lattice energy of an ionic compound depends upon A class 11 chemistry JEE_Main

As a result of isobaric heating Delta T 72K one mole class 11 physics JEE_Main

The graph of current versus time in a wire is given class 12 physics JEE_Main

If a wire of resistance R is stretched to double of class 12 physics JEE_Main

A 5m long pole of 3kg mass is placed against a smooth class 11 physics JEE_Main




