Question

Distinguish between dot product and cross product.

Answer 1

Hint: Product of two vectors can be of two types, Dot product and cross product. Performing either of the two on two vectors, that is, dot product or cross product, one obtains a scalar or vector quantity as a result.

Complete step by step answer:
The quantities which are completely specified by both magnitude as well as direction are known as vector quantities. Whereas the quantities which are completely specified by the magnitudes only are known as scalar quantities.

A vector can be multiplied using two basic types of products. These products are the dot product and the cross product, and they have many differences.

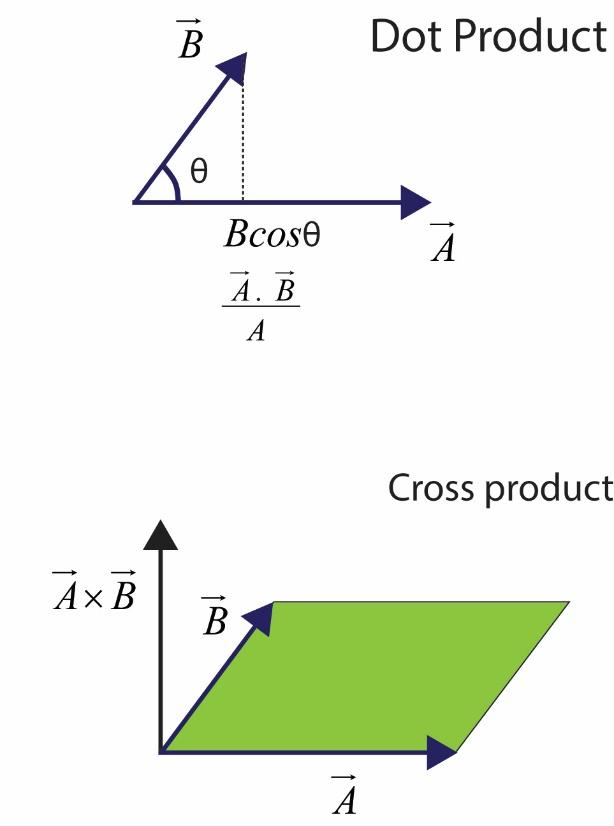
A dot product of two vectors is also called the scalar product. It is the product of the magnitude of the two vectors and the cosine of the angle that they form with each other.
A cross product of two vectors is also called the vector product. It is the product of the magnitude of the two vectors and the sine of the angle that they form with each other.
The difference between the dot product and the cross product of two vectors is that the result of the dot product is a scalar quantity, whereas the result of the cross product is a vector quantity.

Additional Information:
(i)Dot product: A dot product or scalar product of two vectors is the product of their magnitudes and the cosine of the angle subtended by one vector over the other. It is also called the inner product or the projection product. It is represented as:

\[\overrightarrow{A}.\overrightarrow{B}=\left| A \right|\left| B \right|\cos \theta \]

The result is a scalar quantity, so it has only magnitude but no direction.

(ii)Cross product: A cross product or vector product of two vectors is the product of their magnitudes and the sine of the angle subtended by one over the other. It is also called the directed area product. It is represented as:

\[\overrightarrow{A}\times \overrightarrow{B}=\left| A \right|\left| B \right|\sin \theta \hat{z}\]

The result is another vector quantity. The resultant vector direction \[\hat{z}\] is perpendicular to both the vectors. Its direction can be determined using the right–hand rule.

Note: Students should understand the physical significance of both types of products that is dot product and cross product so that they will not confuse between these products. Students should keep in mind that the vector product of two quantities is a vector quantity in itself so they must always represent with the direction.