
What does a dot product equal to one mean?
Answer
481.8k+ views
Hint: We need to have a basic idea of what a dot product actually means. There are many definitions of dot products. We use the basic definition which states dot product or scalar product is given by: \[\left| A \right| \cdot \left| B \right| = \left| A \right| \cdot \left| B \right|\cos \theta \] where \[\theta \] is the angle between two given vectors.
Complete step by step solution:
The dot product is also called a scalar product. This states that multiplying any two vectors will give us a single vector which is scalar. Here we have considered the vectors as A and B
Scalar product or dot product is basically defined as a product of 2 vectors along with the angle of cosine between them. Look at the formula above , we have written 2 terms \[\left| A \right|and\left| B \right|\], these are called magnitudes of vectors(it is the length of the vector).
According to the question they have given that the dot product is 1. It means that \[A \cdot B = 1\]
Or, \[\left| A \right| \cdot \left| B \right|\cos \theta = 1\]
This is possible only when : \[\cos \theta = 0\],
And \[\cos \theta = 0\] , means that the angle between the 2 vectors A and B is zero.
Hence the 2 vectors are parallel. To get better idea look at the image shown below:
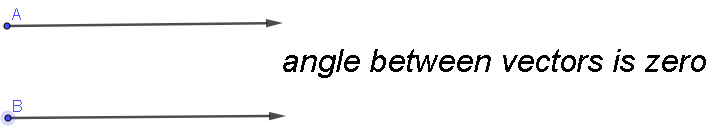
Now the fact that the angle between 2 vectors is 0 means that the vector could be parallel or antiparallel as shown in the image below;

Hence if the dot product is 1 it means that the two given vectors are parallel. And if the dot product is -1 it means that the two given vectors are antiparallel.
Additional Information:
\[ \bullet \] If the angle between 2 given vectors is \[{90^ \circ }\]it means that \[A \cdot B = 0\] and they are said to be orthogonal.
\[ \bullet \] he dot product of a unit vector with itself is given by: \[i \cdot i = j \cdot j = k \cdot k = 1\]
Note:
We should remember that the angle being 0 doesn’t mean that the vectors are only parallel; they can also be antiparallel. Thus when the dot product is 1 it means the vectors are parallel and when the dot product is-1 it means the vectors are anti-parallel.
Complete step by step solution:
The dot product is also called a scalar product. This states that multiplying any two vectors will give us a single vector which is scalar. Here we have considered the vectors as A and B
Scalar product or dot product is basically defined as a product of 2 vectors along with the angle of cosine between them. Look at the formula above , we have written 2 terms \[\left| A \right|and\left| B \right|\], these are called magnitudes of vectors(it is the length of the vector).
According to the question they have given that the dot product is 1. It means that \[A \cdot B = 1\]
Or, \[\left| A \right| \cdot \left| B \right|\cos \theta = 1\]
This is possible only when : \[\cos \theta = 0\],
And \[\cos \theta = 0\] , means that the angle between the 2 vectors A and B is zero.
Hence the 2 vectors are parallel. To get better idea look at the image shown below:
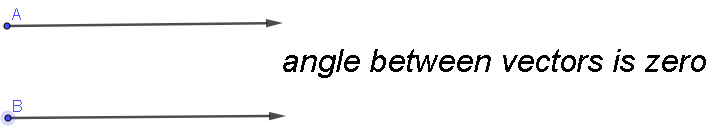
Now the fact that the angle between 2 vectors is 0 means that the vector could be parallel or antiparallel as shown in the image below;

Hence if the dot product is 1 it means that the two given vectors are parallel. And if the dot product is -1 it means that the two given vectors are antiparallel.
Additional Information:
\[ \bullet \] If the angle between 2 given vectors is \[{90^ \circ }\]it means that \[A \cdot B = 0\] and they are said to be orthogonal.
\[ \bullet \] he dot product of a unit vector with itself is given by: \[i \cdot i = j \cdot j = k \cdot k = 1\]
Note:
We should remember that the angle being 0 doesn’t mean that the vectors are only parallel; they can also be antiparallel. Thus when the dot product is 1 it means the vectors are parallel and when the dot product is-1 it means the vectors are anti-parallel.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




