
Answer
433.2k+ views
Hint: Since the mass of each ball is the same, it is the same as saying that the mass of a moving ball is constant from collision to collision. And, velocity of the moving balls right before the collision and that of the balls on the other side after collision are equal. So, for unchanged mass and velocity just before and after collision, the momentum has to be conserved.
Complete step by step answer:
The Newton’s cradle is a tool that demonstrates the conservation of momentum and conservation of energy in a reasonably elastic condition, using four or more vibrating balls. When one ball on the stop is lifted and released at the end, it hits the stationary balls and transfers a force through the stationary balls pushing the last ball. The last ball swings back and hits the almost stationary balls, the effect going in the opposite direction is repeated.
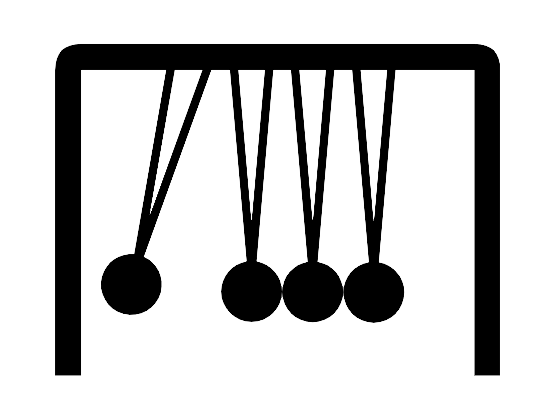
When the first ball hits the second one, it moves in a specific direction. For example, say, it moves from east to west. This means the momentum is also moving to the west. When the direction of motion changes, the momentum changes too, but this cannot happen without any force from outside. Not only the ball $1$ bounce off ball $2$ , but momentum carries the energy westward through all the balls.
But, there is a confusion. The ball will stop for a small time, but definitely at the top of that arc. If motion is required for momentum, how it is preserved! Here, the cradle seems to break the unbreakable law, but the reason it doesn’t is, the law of conservation works only in closed systems. A closed system is one, on which there works no external force. So, Newton's cradle is not a closed system. When we swing out away the ball $5$ from the rest of the balls, the ball also swings up, which slows down the ball under the influence of gravity.
The horizontal line of the balls at rest acts as a closed system, not affected by any force other than gravity. It is here, in the small amount of time between the impact of the first ball and the last swinging, that momentum is conserved.
When the ball reaches its peak, its kinetic energy and momentum drop to zero, and it contains only potential energy. Now, gravity starts to pull the ball down, starting the cycle again.
Note: Newton’s cradle has to be cautiously packaged, because, although this demo is simple, it can be easily damaged by tangling the balls. This is the simplest example of conservation of momentum and this demo makes it more complicated by having different masses.
Complete step by step answer:
The Newton’s cradle is a tool that demonstrates the conservation of momentum and conservation of energy in a reasonably elastic condition, using four or more vibrating balls. When one ball on the stop is lifted and released at the end, it hits the stationary balls and transfers a force through the stationary balls pushing the last ball. The last ball swings back and hits the almost stationary balls, the effect going in the opposite direction is repeated.

When the first ball hits the second one, it moves in a specific direction. For example, say, it moves from east to west. This means the momentum is also moving to the west. When the direction of motion changes, the momentum changes too, but this cannot happen without any force from outside. Not only the ball $1$ bounce off ball $2$ , but momentum carries the energy westward through all the balls.
But, there is a confusion. The ball will stop for a small time, but definitely at the top of that arc. If motion is required for momentum, how it is preserved! Here, the cradle seems to break the unbreakable law, but the reason it doesn’t is, the law of conservation works only in closed systems. A closed system is one, on which there works no external force. So, Newton's cradle is not a closed system. When we swing out away the ball $5$ from the rest of the balls, the ball also swings up, which slows down the ball under the influence of gravity.
The horizontal line of the balls at rest acts as a closed system, not affected by any force other than gravity. It is here, in the small amount of time between the impact of the first ball and the last swinging, that momentum is conserved.
When the ball reaches its peak, its kinetic energy and momentum drop to zero, and it contains only potential energy. Now, gravity starts to pull the ball down, starting the cycle again.
Note: Newton’s cradle has to be cautiously packaged, because, although this demo is simple, it can be easily damaged by tangling the balls. This is the simplest example of conservation of momentum and this demo makes it more complicated by having different masses.
Recently Updated Pages
Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE




