
Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Answer
498.6k+ views
Hint: Here, we will first use that the Euclid’s fifth postulate is if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles and then prove it by using the graph and angles.
Complete step-by-step answer:
We know that the Euclid’s fifth postulate is if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
It says that if
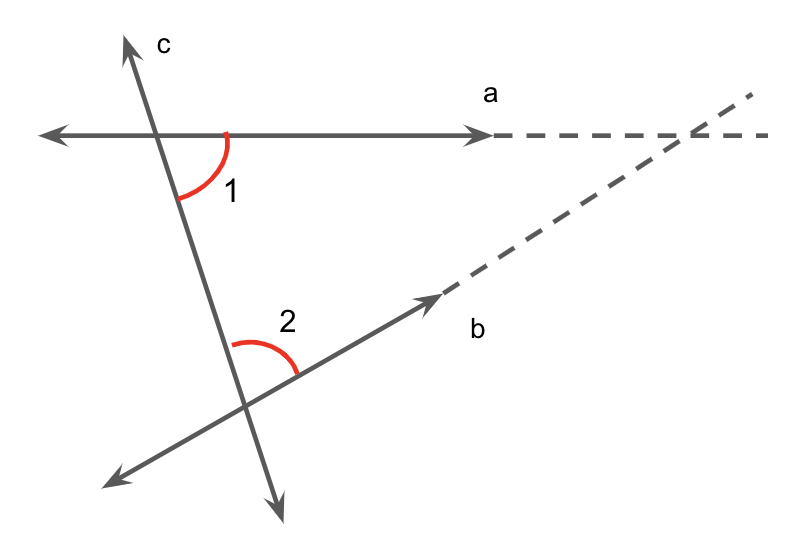
Therefore, by Euclid’s fifth postulate, line
Similarly, we have
Hence, by Euclid’s fifth postulate, line
Thus, Euclid’s postulate implies the existence of parallel lines.
Note: While solving these types of questions, students should know that a statement is an axiom, which is taken to be true without proof and postulates are the basic structure from which lemmas and theorems are derived. We need to know about the Euclid’s postulates before finding the solution of the problem.
Complete step-by-step answer:
We know that the Euclid’s fifth postulate is if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
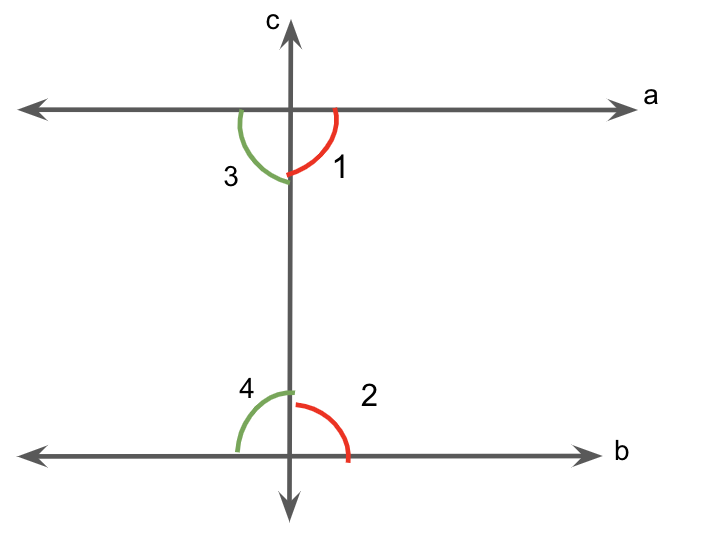
It says that if

Now since we know that

Therefore, by Euclid’s fifth postulate, line
Similarly, we have
Hence, by Euclid’s fifth postulate, line
Thus, Euclid’s postulate implies the existence of parallel lines.
Note: While solving these types of questions, students should know that a statement is an axiom, which is taken to be true without proof and postulates are the basic structure from which lemmas and theorems are derived. We need to know about the Euclid’s postulates before finding the solution of the problem.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




