Question

Why does gravitational potential energy always have a negative sign? Also explain the graph of variation of gravitational potential energy with distance \[r\] from the centre of the earth?

Answer 1

Hint:The capacity to work is defined as energy. The energy possessed by a body due to its shape or position is known as potential energy. The potential energy possessed by the item as a result of Earth's gravity is to blame for this outcome. Gravitational potential energy is the name given to the energy generated by Earth's gravity.

Complete step by step answer:
At the Earth's surface, gravitational potential energy is negative because the gravitational field performs work in bringing a mass from infinity, i.e. work must be performed on a body if it is removed from the earth's gravitational field. As a result, potential energy is negative.
Gravitational potential function inside Earth.
As we approach the sphere's centre, the gravitational field intensity owing to the homogeneous solid sphere within it can be demonstrated to diminish linearly with \[r\] and \[ = 0\] . This is owing to the fact that there is a gravitational attraction between parts of the sphere below the point where another mass is located. Reduce the force between the remaining spherical shell aggregates on the outside to zero.
The gravitational field strength for both inside and outside the sphere is depicted in the diagram below.
The radius of the sphere is \[a\] , while the distance from its centre is \[r\] .

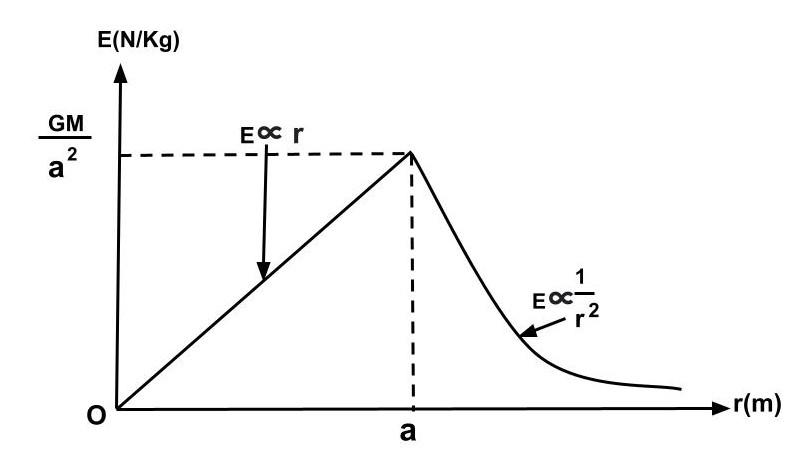
As a result, for distances of \[0\] and \[a\] between the body of mass \[m\] and the sphere, the gravitational field function simplifies to
$E = G\dfrac{{\left( {\dfrac{4}{3}\pi {r^3}\rho } \right)m}}{{{r^2}}}$
Substituting value of density $\rho $ in terms of Mass of the planet $M = \dfrac{4}{3}\pi {a^3}\rho $
\[E = G\dfrac{{\dfrac{4}{3}\pi {r^3}\left( {\dfrac{M}{{\dfrac{4}{3}\pi {a^3}}}} \right)m}}{{{r^2}}}\]
$E = G\dfrac{{Mmr}}{{{a^3}}}$
Gravitational potential function for values of \[r < a\] inside the spherical body will be using procedures identical to those employed in the previous derivation.
$
  U\left( r \right) = - G\dfrac{{{m_r}m}}{r} \\
   \Rightarrow U\left( r \right) = - G\dfrac{{Mm{r^2}}}{{{a^3}}}.......\left( 1 \right) \\
 $
Where ${m_r}$ ​is mass of smaller sphere of radius $r$
Gravitational potential function outside Earth.
We know that the formula for the gravitational potential energy function outside a spherical body is
$U\left( r \right) = - G\dfrac{{Mm}}{r}......\left( 2 \right)$
Which has a value on the planet's surface
$U\left( r \right) = - G\dfrac{{Mm}}{a}$
We know that a point's gravitational potential is defined as the work done on a unit mass to move it to that location from $\infty $ (a point remote from all other masses).
Therefore, total Gravitational potential of a body of mass $m$ can be found by sum of integral of equation (1) from $\lim r = \infty \,to\,r = a$ and integral of equation (2) from $\lim r = a\,to\,r = r$
We should also emphasise that, while the gravitational potential function exists, the Potential inside the Earth derived using equation (1) has no physical meaning because it is physically impossible to take unit mass inside the solid earth, do actual measurements, and compare results. This is a purely academic exercise.
As a result, as seen below, a practical point graph is not drawn for values of distances less than the radius of the planet.

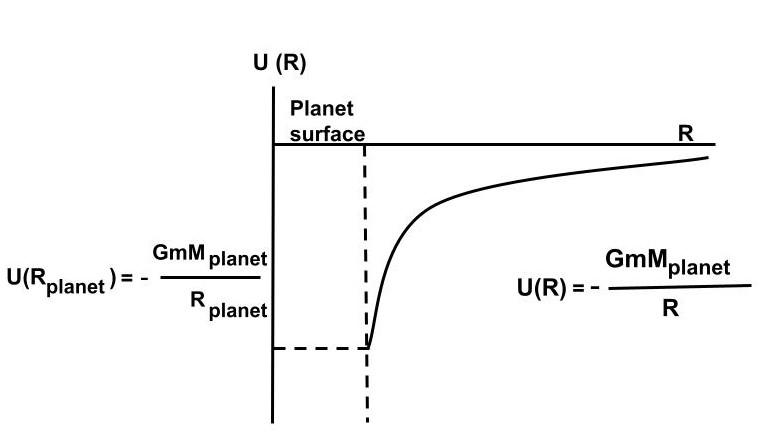
Note:It should be remembered that just the potential at the planet's surface is required for calculations of escape velocity from the earth and computations of satellite orbits, among other things.