Question

What does Tangential force produce?

Answer 1

Hint: In order to answer the above question, we will be discussing the tangential force. We will discuss uniform and non-uniform circular motion and will find out from where does the tangential force arise to reach our answer.

Complete step by step solution:
We all know that the tangential force comes into play when the object is moving in a circular motion or a curved path. Therefore, we will be discussing the case of circular motion to determine our answer.
As we can see from the figure given below,
 

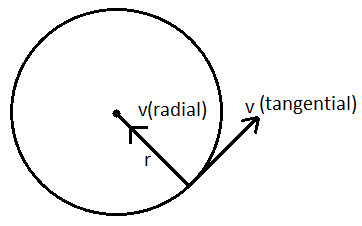
A body is undergoing a circular motion and the radius of the circular path is $r$. This is the basic interpretation of circular motion. Further, the circular motion is divided into two cases: the uniform circular motion and the non-uniform circular motion. It is very crucial for us to understand both of these cases in detail.
UNIFORM CIRCULAR MOTION
When an object travels at a constant speed around a fixed axis or centre point and travels around a curved path, it retains a constant radial distance from the centre point at all times and moves in a tangent to the curved path, this form of motion is seen.
In a uniform circular motion, the velocity of the object remains constant and hence, there is no acceleration. Therefore, there will be no amount of force acting on the particle other than the centripetal force which arises due to the constant change in the direction of radial velocity. The only force needed to hold an object moving in a circular motion at a constant pace is a centripetal force, ${{F}_{c}}$, directed towards the circle's centre.

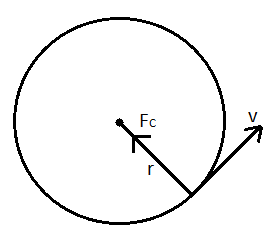
NON-UNIFORM CIRCULAR MOTION
We see that the non-uniform circular motion signifies a change in the particle's speed as it moves along the circular direction. Take careful note of the change in velocity vector sizes, which indicates a change in velocity magnitude.

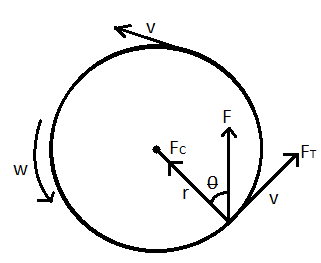
This change in the magnitude of the tangential component of velocity results in a force acting in the tangential direction of the curve. This force is known as the tangential force (${{F}_{T}}$).
Based on all the information, we can imagine two possibilities that the tangential force can produce:
> The circle's radius remains constant (like in the motion along a circular rail or motor track). The magnitude of radial acceleration changes as v changes. This implies that, as with uniform circular motion, the centripetal acceleration is not constant. The radial acceleration increases as the speed increases. When the radius of the circular path is constant, a particle moving faster would require more radial force to change direction, and vice versa.
> The centripetal (radial) force is constant (like a satellite rotating about the earth under the influence of a constant force of gravity). In response to changes in speed, the circular motion varies its radius. This implies that, unlike uniform circular motion, the radius of the circular path is variable. In any case, the centripetal acceleration equation in terms of "speed" and "radius" need to be satisfied.
The above two cases can be produced by a tangential force. Either it can change the radius of the circular path or it can change the radial velocity and cause the magnitude of centripetal force to change instantaneously.

Note:
The crucial thing to remember here is that, while particle speed influences radial acceleration, radial or centripetal force has no effect on particle speed. To change the magnitude of a tangential velocity, we need a tangential power. Tangential acceleration is the name given to the related acceleration.