Question

Where does the center of mass of uniform Triangular lamina lie?

Answer 1

Hint: Centre of mass is always supposed to be in its geometric center if the distribution of the mass is uniform. The Centre of mass is the point at which the entire mass of the body is concentrated. The center of mass is a point that is defined relative to an object or system of objects. It is the average position of all the parts of the system that are weighted according to their masses.


Complete step by step solution:
Consider the fig given

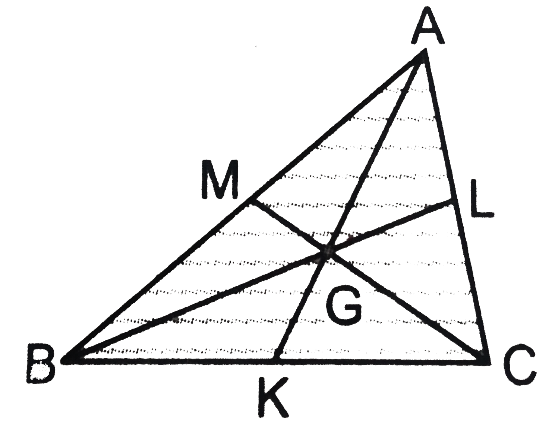
In Fig. ABC is a uniform triangular lamina. It may be subdivided into thin strips, each parallel to the base BC as shown. By symmetry, each strip has its center of mass at its geometrical center. If these points are joined, we get the median AK. Similarly, we can argue that the center of mass lies on median BL and also on median CM. It means the center of mass of uniform triangular lamina lies at the point of intersection of the three medians, i.e., on the centroid GG of the triangle.
The center of mass of the triangular lamina is at the centroid which is the point of the intersection of medians. A median will divide the lamina into two triangles of the same area. Thus equal mass is distributed about the medians.

Note:Sometimes the center of mass doesn't fall anywhere on the object. For simple and rigid objects having a uniform density. The center of mass is situated at the centroid. The centroid is \[\dfrac{{l\sqrt 3 }}{6}\] away from the center of one of the sides in a direction perpendicular to that side and towards that of the interior of the triangle.