Question

Where does the centre of mass of uniform triangular lamina lie?

Answer 1

Hint:Centre of mass is always at Geometrical center if made distribution is uniform. Centre of mass is the point where the body's whole mass is supposed to be concentrated.

Complete step by step answer:
Centre of Mass of a Triangular Lamina: Consider a triangular lamina ABC. Let EG be a thin strip parallel to the side BC. Fig. Since EG is an elemental strip, it can

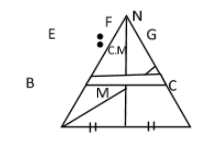
Imagined to be a rod and its c.m. lies at its midpoint F (say). Similarly, we can consider innumerable elemental strips of the form of EG, each parallel to the side BC. The centre of mass of each strip would be at their respective mid points. Evidently, the center of mass of the different strips would line on the median AM of the triangle. Thus, all the strips could be replaced by point masses placed along the median AM and c.m. of all these masses must lie somewhere on AM. Next, we can proceed to consider elemental strips parallel to the side AC and by similar argument, the c.m. of a triangular lamina simultaneously lie on the three medians of the triangle, it should coincide with the point of intersection of the medians i.e. the centroid of the triangle. Thus, the c.m. of a triangular lamina lies on AM, BN etc. dividing them internally in the respective ratio of $2:1$

Note: The weight (W) acting due to a triangular lamina can be replaced by three equal weight's $\left( {\dfrac{W}{3}} \right)$ each, situated at the vertices (corners) or at the mid points of sides of the triangle.