
What does the graph of the seventh root of unity look like on a unit circle?
Answer
443.1k+ views
Hint: For calculating the position of seven roots of unity on a unit circle, we will us Euler’s form of complex numbers which is given by
Then we will plot those points on the Argand’s plane and join those points together to get the required figure.
For a complex number z,
For
Complete step by step solution:
We have,
Taking modulus on both sides,
As we know that
For different values of k, we will get different roots of unity.
For k=0
For k=1,
For k=2,
.
.
.
For k=6,
For k=7, we will return back to the first root of unity lying on the real axis.
Now, plotting these points on the Argand’s plane, we get
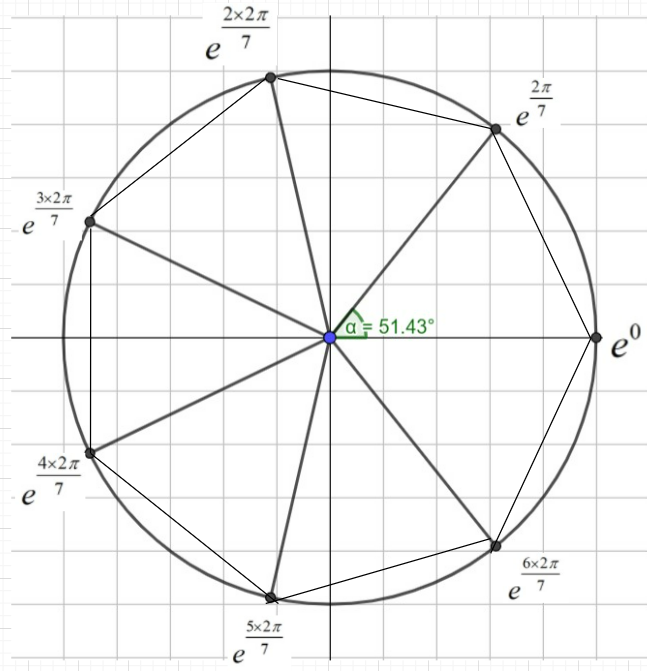
So, on joining the seven roots of unity lying on a circle of unit radius, we get a regular seven-sided polygon.
Note: Each
Then we will plot those points on the Argand’s plane and join those points together to get the required figure.
For a complex number z,
For
Complete step by step solution:
We have,
Taking modulus on both sides,
As we know that
For different values of k, we will get different roots of unity.
For k=0
For k=1,
For k=2,
.
.
.
For k=6,
For k=7, we will return back to the first root of unity lying on the real axis.
Now, plotting these points on the Argand’s plane, we get

So, on joining the seven roots of unity lying on a circle of unit radius, we get a regular seven-sided polygon.
Note: Each
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




