
Why does the value of ‘g’ decrease as we go deep inside a mine (or the Earth)?
Answer
510.6k+ views
Hint: The effective mass of the earth decreases as we go deep inside the earth. As the gravitational force of attraction depends on the mass of earth as well. The mass of earth depends with respect to the third power of radius and the force of attraction varies with respect to the square of radius. As a result, the decrease in mass is more effective.
Formula Used:
The gravitational acceleration is given by,
Complete step-by-step answer:
Consider the following diagram:
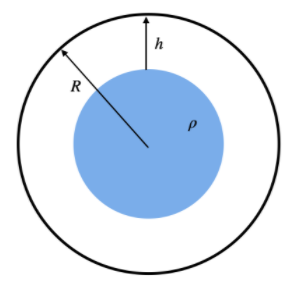
Let’s assume the density of earth is
The radius of earth is R.
Hence, the volume of Earth is,
So, we can write the mass of earth as,
The gravitational acceleration is given by,
So, we can write the gravitational acceleration as,
Hence, the gravitational acceleration varies linearly with respect to the radius.
Now, if we move inside a cave or into the Earth, the effective radius of the earth decreases.
According to Gauss's law, the segment of earth outside that depth will not affect the gravitational force of attraction there.
Hence, we can ignore the effect of the remaining segment.
Hence, the gravitational acceleration will solely depend on the core part, which is coloured in blue.
So, the gravitational acceleration at that location is given by,
Hence, the value of ‘g’ decreases as we go deep inside a mine.
Note:We have excluded the effects of the segment of earth outside the coloured part, because it will not have any effect on the gravitational force of attraction. If we consider a spherical shape just outside the coloured segment, it will not have mass of the remaining segment inside the imaginary sphere. Hence, it will not affect the gravitational acceleration.
Formula Used:
The gravitational acceleration is given by,
Complete step-by-step answer:
Consider the following diagram:

Let’s assume the density of earth is
The radius of earth is R.
Hence, the volume of Earth is,
So, we can write the mass of earth as,
The gravitational acceleration is given by,
So, we can write the gravitational acceleration as,
Hence, the gravitational acceleration varies linearly with respect to the radius.
Now, if we move inside a cave or into the Earth, the effective radius of the earth decreases.
According to Gauss's law, the segment of earth outside that depth will not affect the gravitational force of attraction there.
Hence, we can ignore the effect of the remaining segment.
Hence, the gravitational acceleration will solely depend on the core part, which is coloured in blue.
So, the gravitational acceleration at that location is given by,
Hence, the value of ‘g’ decreases as we go deep inside a mine.
Note:We have excluded the effects of the segment of earth outside the coloured part, because it will not have any effect on the gravitational force of attraction. If we consider a spherical shape just outside the coloured segment, it will not have mass of the remaining segment inside the imaginary sphere. Hence, it will not affect the gravitational acceleration.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




