
Answer
436.8k+ views
Hint: Recall that torque is associated with rotational motion whereas force is most often related to linear motion. Additionally, we know that torque is a result of a force acting on an object. To this end, determine how the two are definitively distinct and how you can compare the two using a simple example, say in the context of a wrench tightening a bolt.
Complete Solution:
Let us begin by first understanding force and torque and a comparison between them following which we shall establish a distinction between the two using an example.
A force can simply be defined as any interaction that may change the state of rest or motion of an object. A force usually becomes a contributing factor to such a change in a system when it is significantly unopposed and the net force acting on the system is not equal to zero. Force is a vector quantity since it is usually associated with a direction in which it acts, along with the magnitude of the force applied. The SI unit of measurement of force is Newton $(N)$, which is defined as the amount of force that is required to displace a mass of $1\;kg$ with an acceleration of $1\;ms^{-2}$. Force is usually associated with the linear acceleration of objects.
Torque on the other hand, is the rotational equivalent of linear force. Torque accounts for any angular motion that is produced as a result of the application of a linear force. It is defined as a twisting force that tends to cause torsion or rotation of an object about an axis or a fixed point. Torque is a pseudovector in a sense that in addition to a magnitude, it has a sign-based direction (opposite signs for clockwise and anticlockwise rotations). The SI unit of torque is Newton-meter (N-m), which is defined as the torque resulting from a force of $1\;N$ applied perpendicularly at a distance of $1\;m$ from the axis of rotation. Torque is usually associated with the angular acceleration of objects.
Now, let us try and establish the distinction between torque and force from the following example.
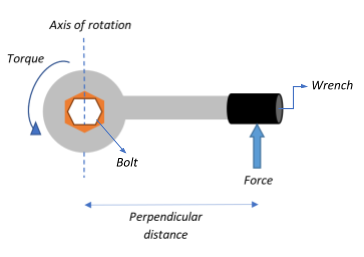
Consider a wrench placed around a bolt. To tighten the bolt, by applying a linear force about the handle of the wrench at a distance perpendicular to the axis of rotation, we are able to produce a rotational motion about the bolt which is nothing but the torque acting on the bolt. Quantitatively, if F is the force applied on the wrench at a distance $r_{\perp}$ from the axis of rotation, then torque.
$\tau = r_{\perp} \times F$.
Note:
It is important to keep in mind that since torque is a pseudovector in three dimensions, it is usually defined as the cross product of the position vector $\vec{r}$ and the force vector $\vec{F}$. Thus, the torque $\tau$ acting on an object depends upon three factors: the applied force $\vec{F}$, the position vector connecting the axis of rotation and the point of application of force $\vec{r}$, and the angle between the force and the position vector, $\theta$. This is physically described as:
$\tau = \vec{r} \times \vec{F} = |\vec{r}||\vec{F}|sin\;\theta$.
Also, do not get confused between N-m and N.m, where N-m is the unit of torque, whereas N.m is the unit of energy (joule).
Complete Solution:
Let us begin by first understanding force and torque and a comparison between them following which we shall establish a distinction between the two using an example.
A force can simply be defined as any interaction that may change the state of rest or motion of an object. A force usually becomes a contributing factor to such a change in a system when it is significantly unopposed and the net force acting on the system is not equal to zero. Force is a vector quantity since it is usually associated with a direction in which it acts, along with the magnitude of the force applied. The SI unit of measurement of force is Newton $(N)$, which is defined as the amount of force that is required to displace a mass of $1\;kg$ with an acceleration of $1\;ms^{-2}$. Force is usually associated with the linear acceleration of objects.
Torque on the other hand, is the rotational equivalent of linear force. Torque accounts for any angular motion that is produced as a result of the application of a linear force. It is defined as a twisting force that tends to cause torsion or rotation of an object about an axis or a fixed point. Torque is a pseudovector in a sense that in addition to a magnitude, it has a sign-based direction (opposite signs for clockwise and anticlockwise rotations). The SI unit of torque is Newton-meter (N-m), which is defined as the torque resulting from a force of $1\;N$ applied perpendicularly at a distance of $1\;m$ from the axis of rotation. Torque is usually associated with the angular acceleration of objects.
Now, let us try and establish the distinction between torque and force from the following example.

Consider a wrench placed around a bolt. To tighten the bolt, by applying a linear force about the handle of the wrench at a distance perpendicular to the axis of rotation, we are able to produce a rotational motion about the bolt which is nothing but the torque acting on the bolt. Quantitatively, if F is the force applied on the wrench at a distance $r_{\perp}$ from the axis of rotation, then torque.
$\tau = r_{\perp} \times F$.
Note:
It is important to keep in mind that since torque is a pseudovector in three dimensions, it is usually defined as the cross product of the position vector $\vec{r}$ and the force vector $\vec{F}$. Thus, the torque $\tau$ acting on an object depends upon three factors: the applied force $\vec{F}$, the position vector connecting the axis of rotation and the point of application of force $\vec{r}$, and the angle between the force and the position vector, $\theta$. This is physically described as:
$\tau = \vec{r} \times \vec{F} = |\vec{r}||\vec{F}|sin\;\theta$.
Also, do not get confused between N-m and N.m, where N-m is the unit of torque, whereas N.m is the unit of energy (joule).
Recently Updated Pages
Fill in the blanks with suitable prepositions Break class 10 english CBSE

Fill in the blanks with suitable articles Tribune is class 10 english CBSE

Rearrange the following words and phrases to form a class 10 english CBSE

Select the opposite of the given word Permit aGive class 10 english CBSE

Fill in the blank with the most appropriate option class 10 english CBSE

Some places have oneline notices Which option is a class 10 english CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

When was Karauli Praja Mandal established 11934 21936 class 10 social science CBSE

Which are the Top 10 Largest Countries of the World?

What is the definite integral of zero a constant b class 12 maths CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Distinguish between the following Ferrous and nonferrous class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




