Question

What is the domain and range of \[y = \cos \left| x \right|\]?

Answer 1

Hint: In order to solve this question, we have to find the domain and range of a given function. The domain is the values of x coordinate on which we get the real and finite value of y. The range is the values of y which are obtained by putting all the values of x. To solve this question first we break the function into different domains and check on all the parts. And find that there is no difference in normal function and the given function. So the domain and range of that function are the same as the normal trigonometry function.

Complete step-by-step answer:
\[\cos \left| x \right|\] is the \[\cos x\]function with the absolute value of \[x\] input into it. Meaning of absolute value is that if \[x \geqslant 0\] then it is replaced with \[x\]. If \[x < 0\] then it is replaced with \[ - x\].
Here \[\cos \] is an even function. Even function is the function that is the mirror on the y axis and in other words, we can say that if we replace the value with the negative sign then the function remains the same then that function is known as even function.
This means that:
\[f\left( x \right) = \left\{ \begin{gathered}
  \cos \left| x \right| = \cos \left( x \right)\,\,if\,x \geqslant 0 \\
  \cos \left| x \right| = \cos \left( { - x} \right)\,\,if\,x < 0\, \\
\end{gathered} \right\}\]
So \[\cos \left| x \right| = \cos x\]
The domain and range will be precisely the same as for the original function, that is: \[x\] can be all real numbers, and \[y\] will range from -1 to 1.
We can see the graph also.

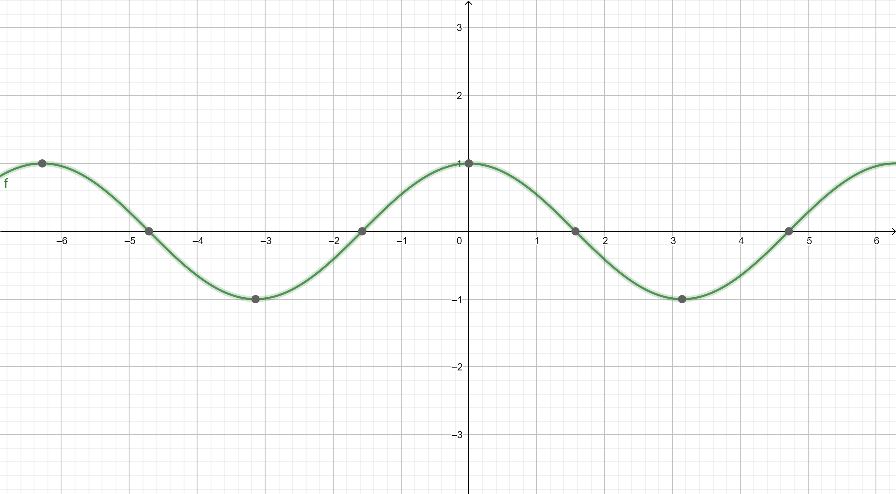
Final answer:
Domain of the function \[y = \cos \left| x \right|\] is \[ \in \left( { - \infty ,\infty } \right)\]
The range of the function is from -1 to 1.

Note: In order to solve this type of question first, we check the function in negative and positive values and then we check the range of the function. Students commit mistakes in these types of questions in breaking the interval of the domain and they are also confused in domain and range. They exchange both parts.