
Why don’t two equipotential surfaces intersect each other?
Answer
494.1k+ views
Hint: Equipotential surfaces cannot intersect at any point. Such a situation is impossible and non-existing. If such a situation arises then at a single point there will be the same physical quantities with different directions and magnitudes, which is not possible.
Complete answer:
Equipotential surfaces are those with constant electric potential throughout. The potential is defined as the work done to bring charge from infinity to another charge ‘q’. The electric potential experienced due to a charge q is given by –
When we closely analyse this equation, we can understand that there are an infinite number of ‘P’s in a given space which are at a distance ‘r’ from the charge ‘q’. Obviously, these points when joined together in 2-D gives a circle as shown below -
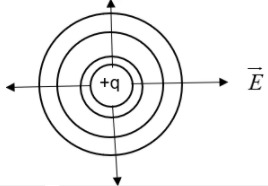
When joined in 3-D, it constitutes a spherical surface. Each circle shows an equipotential surface when taken in 3-D. From the diagram it is clear that the equipotential surfaces never intersect. We can also see that the equipotential surface is perpendicular to the electric field direction. i.e., the potential keeps on decreasing as the distance from the source increases and both are related by a factor of ‘r’.
Now, let us consider the situation when two equipotential surfaces intersect, then will see that the electric field strength and electric potential tends to have more than one value, which is unacceptable. For an electric field from more than two charges the equipotential surface is such that it is the vector sum of all the individual surfaces.
Additional Information:
The electric field and potential are related by
Note:
The electric field is always perpendicular to the equipotential surface. The electric field is also constant along the equipotential surface. The two are related such that a foregoing electric field weakens with distance and the potential drops with this.
Complete answer:
Equipotential surfaces are those with constant electric potential throughout. The potential is defined as the work done to bring charge from infinity to another charge ‘q’. The electric potential experienced due to a charge q is given by –
When we closely analyse this equation, we can understand that there are an infinite number of ‘P’s in a given space which are at a distance ‘r’ from the charge ‘q’. Obviously, these points when joined together in 2-D gives a circle as shown below -

When joined in 3-D, it constitutes a spherical surface. Each circle shows an equipotential surface when taken in 3-D. From the diagram it is clear that the equipotential surfaces never intersect. We can also see that the equipotential surface is perpendicular to the electric field direction. i.e., the potential keeps on decreasing as the distance from the source increases and both are related by a factor of ‘r’.
Now, let us consider the situation when two equipotential surfaces intersect, then will see that the electric field strength and electric potential tends to have more than one value, which is unacceptable. For an electric field from more than two charges the equipotential surface is such that it is the vector sum of all the individual surfaces.
Additional Information:
The electric field and potential are related by
Note:
The electric field is always perpendicular to the equipotential surface. The electric field is also constant along the equipotential surface. The two are related such that a foregoing electric field weakens with distance and the potential drops with this.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




