Question

Draw a circle and any two of its diameters. What figure is obtained if the diameters are perpendicular to each other? How do you check your answers?

Answer 1

Hint – In this particular type of question use the concept that the diameter of the circle is always passing through the center of the circle and the two perpendicular diameter always makes a 90 degrees at the center so use these concepts to reach the solution of the question.

Complete step by step solution:
Assume a point O as the center of the circle.
Let us assume that the circle is of radius 4cm.
So take a compass and make the pointed end of the compass at the center and draw a circle of 4 cm radius with the pencil end of the compass as shown in the below figure.

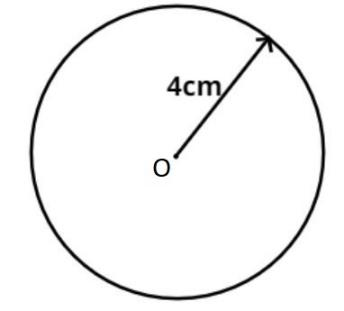
Now as we know that the diameter of the circle is always passing through the center, so draw any two lines passing through the center as shown in the below figure.

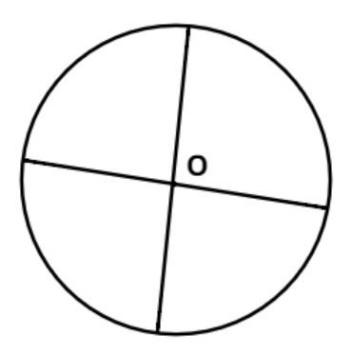
Now draw two perpendicular diameters (i.e. they intersect at 90 degrees), let us assume that these two diameters are AC and BD as shown in the below figure.

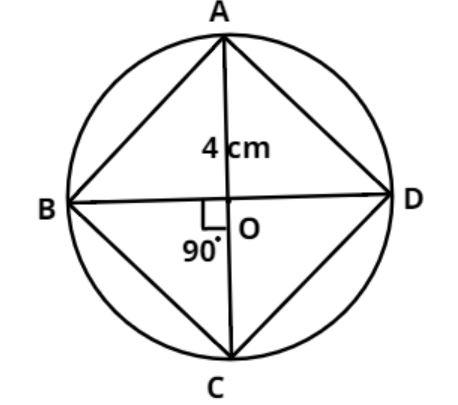
Now join these points together (i.e. A to B, B to C, C to D and D to A) as shown in the figure.
So the figure obtained is a square.
Now we have to verify this.
As the radius of the circle is 4cm. so OA = OB = OC = OD = 4 cm.
And $\angle AOB = \angle BOC = \angle COD = \angle DOA = {90^o}$
So apply Pythagoras theorem in triangle AOB we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
Now substitute the variables we have,
$ \Rightarrow {\left( {{\text{AB}}} \right)^2} = {\left( {{\text{OA}}} \right)^2} + {\left( {{\text{OB}}} \right)^2}$
Now substitute the values we have,
$ \Rightarrow {\left( {{\text{AB}}} \right)^2} = {\left( {\text{4}} \right)^2} + {\left( {\text{4}} \right)^2} = 16 + 16 = 32 = {\left( {4\sqrt 2 } \right)^2}$
$ \Rightarrow {\text{AB}} = 4\sqrt 2 $ cm.
Similarly,
$ \Rightarrow {\left( {{\text{BC}}} \right)^2} = {\left( {{\text{OB}}} \right)^2} + {\left( {{\text{OC}}} \right)^2}$
$ \Rightarrow {\text{BC}} = 4\sqrt 2 $cm.
$ \Rightarrow {\left( {CD} \right)^2} = {\left( {{\text{OC}}} \right)^2} + {\left( {{\text{OD}}} \right)^2}$
$ \Rightarrow CD = 4\sqrt 2 $ cm.
$ \Rightarrow {\left( {DA} \right)^2} = {\left( {{\text{OD}}} \right)^2} + {\left( {{\text{OA}}} \right)^2}$
$ \Rightarrow D{\text{A}} = 4\sqrt 2 $ cm.
So as we see that AB = BC = CD = DA and all diagonals of this square (i.e. AC and BD) are perpendicular to each other so ABCD is a square.
Hence verified.

Note – Whenever we face such types of questions the key concept we have to remember is that always recall the Pythagoras theorem that square of the hypotenuse is equal to the sum of the square of the perpendicular and the square of the base so using this theorem we can verify what figure ABCD is, as above verified.