Question

Draw a circle of radius 5cm. From a point 8cm away from the centre, construct two tangents to the circle. Measure them. ( write the steps of construction )

Answer 1

Hint: Tangent is that line of a circle that touches at a circle on exactly one point but it never enters the interior circle. Here we must know that the radius and tangent are always perpendicular to each other

Complete step-by-step answer:
Now let us solve this construction problem step by step so that we will understand it properly.
And for that we had to name the centre of circles so let us assume that the circle with radius 5cm centre as P and the circle with radius 8cm centre as Q.
Step 1. First of all, let us draw a circle of radius 5cm ( centre P ) with the help of a compass.
Step 2. Now mark a point outside the circle named Q and remember that the distance of Q from the centre P must be 8cm.
Step 3. Mark an arc from point P and Q to draw a perpendicular bisector of line segment PQ. And then mark the midpoint ( A ) of PQ.
Step 4. Now draw a circle which has A as its centre and AP as its radius and that circle must intersect the circle with P at some points ( let say M and N ).
Step 5. Now join the point that we had taken outside the circle with the intersecting points ( i.e. join QM and QN ).
And so the QM and QN are the required tangents.

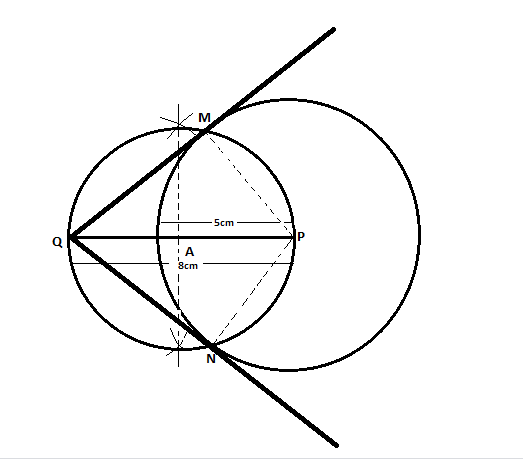
Now we had to measure the tangents QM and QN.
If we join PM and PN so it is equal radius of circle with centre P and as we know that radius of circle is always perpendicular to the tangents so \[QM \bot PM\]and \[QN \bot PN\] and we also know that QP = 8cm
So, now applying Pythagoras theorem in \[\vartriangle PQM\]
\[Q{P^2} = P{M^2} + M{Q^2}\]
\[ \Rightarrow {8^2} = {5^2} + M{Q^2}\]
So, \[ \Rightarrow MQ = \sqrt {{8^2} - {5^2}} = \sqrt {64 - 25} = \sqrt {39} = 6.2cm\]
Hence the tangent MQ = NQ = 6.2cm.

Note:Whenever we had to construct such a type of diagram we must look at the perpendicular bisector of the centre of the circle and the exterior point that we had taken. And with the midpoint of that perpendicular bisector we had to draw another circle and only then we will be able to draw or construct the tangents because the tangents must be from the exterior point that we had taken earlier and also must touch the intersecting points of both the circles.