Question

Draw a circle with center O and radius 3.5cm. Take point P at a distance 5.7 from the center. Draw tangents to the circle from point P.

Answer 1

Hint: In this question, we need to draw tangents to the circle having center O from an exterior point P. For this, we will first join OP and draw its perpendicular bisector. Then from the point at which the bisector cuts the line to the center, we will open the compass and draw a half circle. Point at which this half circle cuts the original circle will be our point of contact of two tangents. Thus joining P to these points will give us our required tangents.

Complete step-by-step answer:
Let us draw the given statements with proper steps of construction.
1: First, let us draw a circle with radius 3.5cm and center O. Now from O let us take a point P in the exterior of the circle such that OP = 5.7cm. Let us join these two points to get line segment OP. We get:

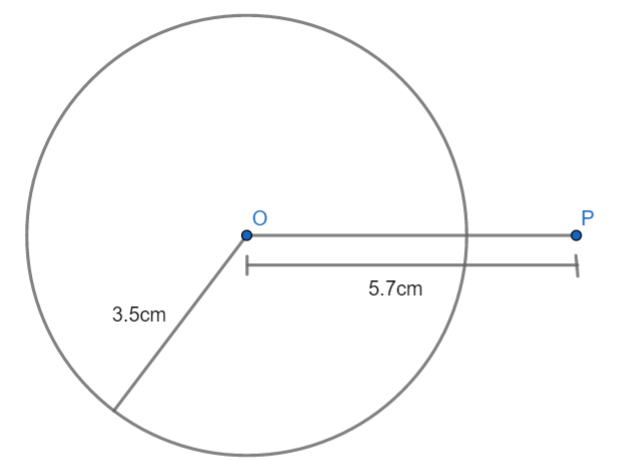
2: Now we need to take OP as diameter to draw a circle which cuts the circle. For this, let us first find the perpendicular bisector of line OP. For finding the perpendicular bisector, we need to open the compass more than half the lines and then mark arc from both ends of the line. The points where these arcs cut are then joined which require a perpendicular bisector. Let the point be M where the bisector cuts the line. We get:

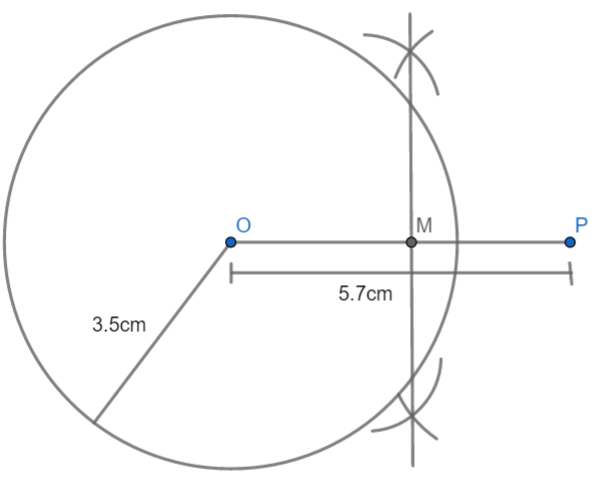
3: Now let us take OM as radius and then draw half of the circle taking M as center. The half circle will cut the original circle at points A and B. These points are points of contact. After that, let us join AP and BP. Thus, we get two tangents to the circle AP and BP. We get:

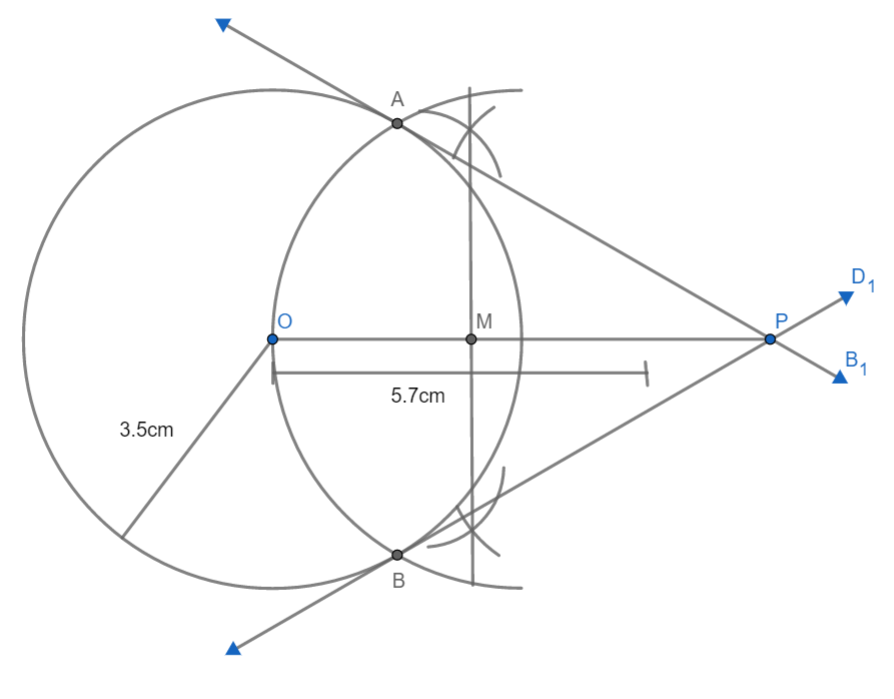
Hence we have drawn our required tangent AP and BP.

Note: Students should note that, distance from O to P is 5.7cm. They can make the mistake of taking distance from the boundary circle to P. Make sure that, compass is tight and the pencil is sharpened. Students can get confused in different arcs.