
Draw a circuit diagram of an electric circuit containing a cell, a key, an ammeter, a resistor of 4 $\Omega$ in series with a combination of two resistors (8 $\Omega$ each) in parallel and a voltmeter across parallel combination. Each of them dissipates maximum energy and can withstand a maximum power of 16W without melting. Find the maximum current that can flow through the three resistors.
Answer
489.6k+ views
Hint We should know that resistors are in the parallel then if their terminals connected to the same two nodes. The equivalent overall resistance is smaller compared to the smallest parallel resistor. Based on this concept we have to solve this question and draw the circuit.
Complete step by step answer:
Here the circuit in which a resistor of resistance 4$\Omega$ is attached in series and two resistors of resistance 8$\Omega$ are attached in parallel. Also, Ammeter and voltmeter attached in the circuit in series and parallel respectively.
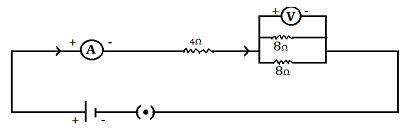
Now, the maximum power of each resistor is 16W
4$\Omega$ resistor is joined in series with the circuit.
So, Power = ${{i}^{2}}R$, here i is current through resistor of resistance R
$16={{i}^{2}}\times 4\Omega$
i = 2A
Now, 2A is passing through parallel resistors of resistance 8$\Omega$.
We know that in parallel potential differences are constant, so the current divides into two parts, due to the same resistance current on each resistance will be half. So, the current passing through each parallel resistor is $\dfrac{2}{2A}=1A$
So, finally current through $4\Omega$ resistor = 2A
Current through each $8\Omega$ resistor = 1A
Note Ammeter is defined as an instrument for the measuring either direct or alternating electric current, in the amperes. An ammeter can measure a wide range of current values because at high values only a small portion of the current is directed through the meter mechanism. A shunt resistance in the parallel connection with the meters carries the major portion.
Complete step by step answer:
Here the circuit in which a resistor of resistance 4$\Omega$ is attached in series and two resistors of resistance 8$\Omega$ are attached in parallel. Also, Ammeter and voltmeter attached in the circuit in series and parallel respectively.

Now, the maximum power of each resistor is 16W
4$\Omega$ resistor is joined in series with the circuit.
So, Power = ${{i}^{2}}R$, here i is current through resistor of resistance R
$16={{i}^{2}}\times 4\Omega$
i = 2A
Now, 2A is passing through parallel resistors of resistance 8$\Omega$.
We know that in parallel potential differences are constant, so the current divides into two parts, due to the same resistance current on each resistance will be half. So, the current passing through each parallel resistor is $\dfrac{2}{2A}=1A$
So, finally current through $4\Omega$ resistor = 2A
Current through each $8\Omega$ resistor = 1A
Note Ammeter is defined as an instrument for the measuring either direct or alternating electric current, in the amperes. An ammeter can measure a wide range of current values because at high values only a small portion of the current is directed through the meter mechanism. A shunt resistance in the parallel connection with the meters carries the major portion.
Recently Updated Pages
Master Class 12 Social Science: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
The gas that burns in oxygen with a green flame is class 12 chemistry CBSE

The probability that a leap year will have only 52 class 12 maths CBSE

Describe the poetic devices used in the poem Aunt Jennifers class 12 english CBSE

And such too is the grandeur of the dooms We have imagined class 12 english CBSE

What does the god that failed refer to class 12 english CBSE

Which country did Danny Casey play for class 12 english CBSE




