Question

Draw a graph for the function:
              \[y=x+|x|\]

Answer 1

Hint: we will make use of the properties of the modulus function to plot the given graph. we will draw the graph of this straight line with the help of \[y=mx+c\text{ }\!\![\!\!\text{ where }m\,\,\text{is slope and }c\text{ is }y-\operatorname{int}ercept\text{ }\!\!]\!\!\text{ }\]


Complete step by step solution:
Before starting the sums we need to understand how the mod function works.
A mod function of \[x\] means that all of its values will be zero when \[x\] is less than 0.and thus all the value of \[x\] will be positive when \[x\] is greater than or equals to 0. Basically, it means that \[x\] wants all the values associated within this mod function to be greater than or equals to 0. \[|x|=\left\{ \begin{align}
  & x\text{ for}\,\,x\ge 0 \\
 & -x\text{ for }x<0 \\
\end{align} \right\}\].
Thus for the equation given to us here we can say that….
\[x+|x|=\left\{ \begin{align}
  & 2x\text{ for}\,\,x\ge 0 \\
 & \text{0 for }x<0 \\
\end{align} \right\}\].
Therefore, when \[x\] is less than 0, then \[y=0,\]therefore we can say that the line will go along the negative \[x\]-axis.
But when \[x\] is positive we see a straight line equation which can be compared to \[y=mx+c\,\,\,\,\,\text{ }\!\![\!\!\text{ where }m\,\,\text{is slope and }c\,\text{is }y-\operatorname{int}ercept\text{ }\!\!]\!\!\text{ }\].
Thus accordingly comparing \[y=mx+c\] to the given equation which is converted to \[y=2x\] when x is positive we can find the slope and the intercept.
Therefore, we find \[m=2\,\,\,\,\text{and }c=0\].
We see that \[y-\operatorname{int}ercept\] is zero which means that the straight line doesn’t intersect with the \[y\]-axis at all.
Thus the graph will be,

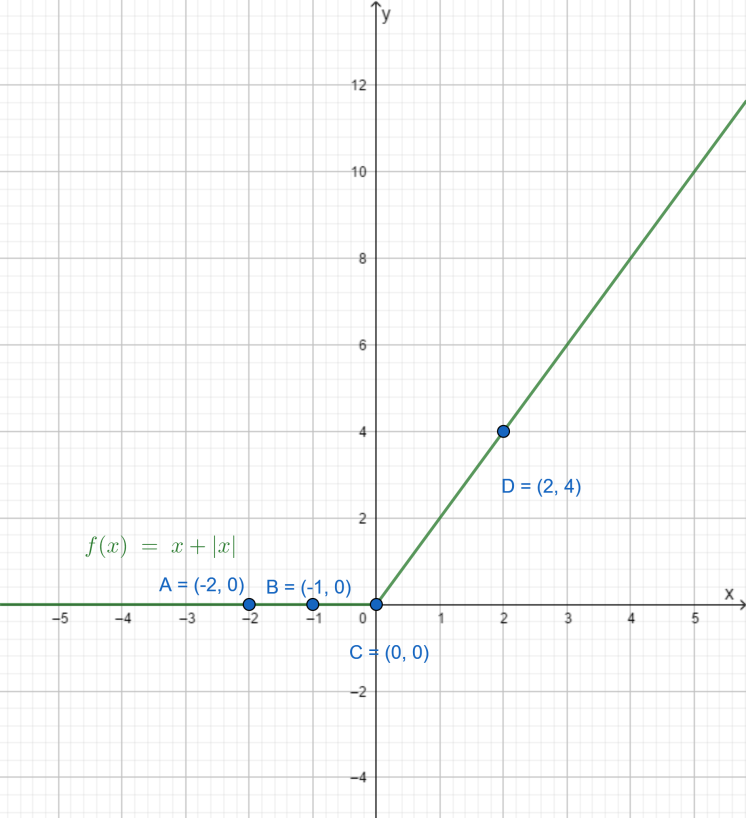
To further verify the graph we can put the values of \[x\] in the equation given to us.
When \[x\] is negative,
\[x=-2\text{ then}\ y=-2+|-2|\] and since mod function will change all the negative values to positive we will be yielded with
\[y=-2+2=0\].
Similarly, when we put
\[\begin{align}
  & x=-1\text{ then}\ y=-1+|-1| \\
 & y=-1+1=0 \\
\end{align}\]
But when we \[x\] is positive,
\[x=2\,\,\text{then}\ y=2+|2|\] and since mod function doesn’t change the value of numbers which are already positive we will be yielded with,
\[y=2+2=4\].



Note: A modulus function is a function that will always yield a positive output. make sure to plot the points exactly in accordance to the values obtained.