Question

Draw a line segment CD. Produce it to CE such that CE = 3CD.

Answer 1

Hint: Draw a line l and take two points C and D on it. Take a divider and open it such that the ends of both of its arms are at C and D. Now, lift the divide and place one end at D and the other end opposite to C at A without changing its length i.e distance between sharp points of the divider. Repeat this step again to get the point E. This is the required construction.

Complete step-by-step answer:
In this question, we need to draw a line segment CD. We then need to produce it to CE such that CE = 3CD.
We draw a line l and take two points C and D on it.
We will now take a divider and open it such that the ends of both of its arms are at C and D. Then, we will lift the divider and place its one end at D and the other end on the line l on the side opposite to point C without changing its length.
Let this point be A.
Now, we will lift the divider again and place its one end at A and the other end on the line l on the side opposite to point C without changing its length.
Name this point as E.
The figure below shows the final construction.

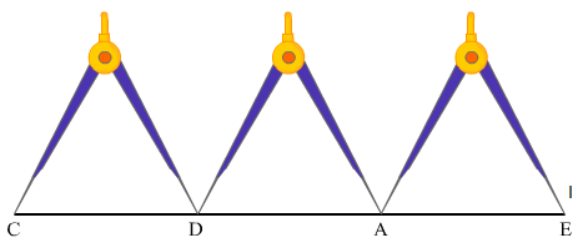
Here we have the following:
CD = DE = AE (because we did not change the length on the divider) …(1)
CE = CD + DE + AE
Substituting equation (1) in this, we will have the following:
CE = CD + CD + CD
CE = 3CD

Note: In this question, it is very important to know what a divider is and how it is used. Dividers are one of the earliest and most basic types of mathematical instruments. In their simplest form, dividers consist of a jointed pair of legs, each with a sharp point. They can be used for geometrical operations such as for taking off and transferring dimensions.