
Draw a ‘more than ogive’ for the following data:
Class 0 – 10 10 – 20 20 – 30 30 – 40 40 – 50 50 – 60 60 – 70 70 – 80 Frequency 5 9 10 12 8 7 5 4
| Class | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| Frequency | 5 | 9 | 10 | 12 | 8 | 7 | 5 | 4 |
Answer
489k+ views
1 likes
Hint: To solve this question we will, first of all, calculate the cumulative frequency of the given data in “more than ogive” form. It is obtained by subtracting first class, second class frequency from the total, third class frequency from total and so on. Finally, we will make an ogive by using a class on the x – axis and ogive on the y-axis.
Complete step by step answer:
Let us first define an Ogive. The Ogive is defined as the frequency distribution graph of a series. The Ogive is a graph of a cumulative distribution that explains data value on the horizontal plane axis and the cumulative relative frequencies, the cumulative frequencies, or the cumulative percent frequencies on the vertical axis.
More than or greater than ogive – the frequencies of the succeeding classes are added to the frequency of a class. This series is called the more than or greater than the cumulative series. It is constructed by subtracting first class, second class frequency from the total, third class frequency from that and so on. The cumulative results in greater than or more than the cumulative series. We are given that data as
We will make a new table having a midpoint of the above given class and also having a column of cumulative frequency (greater than type) which is calculated as theory explained above. We have to add frequency and we get it as 60.
Let us draw the ogive using the midpoint on the x-axis and cumulative frequency on the y-axis.
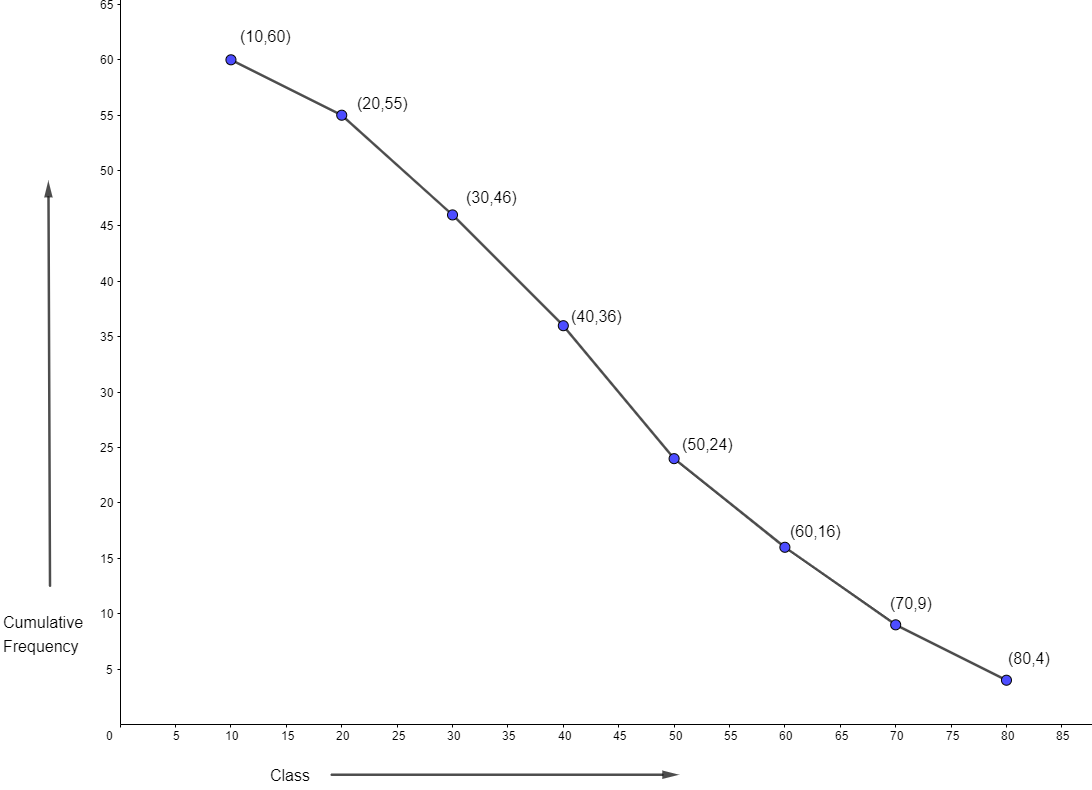
Thus the more than ogive for the given data is obtained.
Note: The graphs of the frequency distribution are frequency graphs that are used to exhibit the characteristics of the discrete and continuous data, such figures are more appealing to the eye than the tabular data. It helps to facilitate the comparative study of two or more frequency distributions. The two methods of Ogive are less than ogive and greater than ogive.
Complete step by step answer:
Let us first define an Ogive. The Ogive is defined as the frequency distribution graph of a series. The Ogive is a graph of a cumulative distribution that explains data value on the horizontal plane axis and the cumulative relative frequencies, the cumulative frequencies, or the cumulative percent frequencies on the vertical axis.
More than or greater than ogive – the frequencies of the succeeding classes are added to the frequency of a class. This series is called the more than or greater than the cumulative series. It is constructed by subtracting first class, second class frequency from the total, third class frequency from that and so on. The cumulative results in greater than or more than the cumulative series. We are given that data as
| Class | Frequency |
| 0 – 10 | 5 |
| 10 – 20 | 9 |
| 20 – 30 | 10 |
| 30 – 40 | 12 |
| 40 – 50 | 8 |
| 50 – 60 | 7 |
| 60 – 70 | 5 |
| 70 – 80 | 4 |
We will make a new table having a midpoint of the above given class and also having a column of cumulative frequency (greater than type) which is calculated as theory explained above. We have to add frequency and we get it as 60.
| Class | Mid-Point | Frequency | Cumulative Frequency |
| 0 – 10 | 5 | 5 | 60 |
| 10 – 20 | 15 | 9 | 55 |
| 20 – 30 | 25 | 10 | 46 |
| 30 – 40 | 35 | 12 | 36 |
| 40 – 50 | 45 | 8 | 24 |
| 50 – 60 | 55 | 7 | 16 |
| 60 – 70 | 65 | 5 | 9 |
| 70 – 80 | 75 | 4 | 4 |
Let us draw the ogive using the midpoint on the x-axis and cumulative frequency on the y-axis.

Thus the more than ogive for the given data is obtained.
Note: The graphs of the frequency distribution are frequency graphs that are used to exhibit the characteristics of the discrete and continuous data, such figures are more appealing to the eye than the tabular data. It helps to facilitate the comparative study of two or more frequency distributions. The two methods of Ogive are less than ogive and greater than ogive.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
EMI starts from ₹3,108.34 per month
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




