Question

Draw a neat and labelled diagram of a suspended moving coil galvanometer. Also, show that the current through an MCG is directly proportional to the deflection of a coil.

Answer 1

Hint: A galvanometer is a device that can detect current in a circuit, it also tells the direction of the current. In a moving coil galvanometer, the coil that carries the current in the circuit is rotated because of change in magnetic flux, this causes a deflection in the scale of MCG.

Formula used:
 $ {T_D} = NIAB\sin \theta $ .

Complete step by step solution:
The following are the labelled diagrams of a suspended moving coil galvanometer-

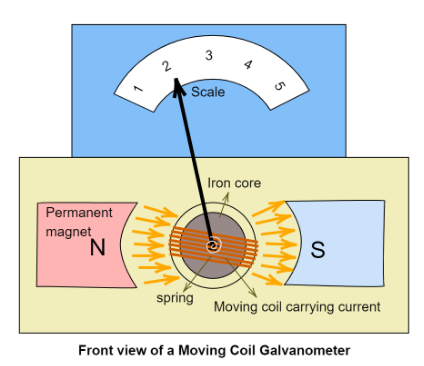
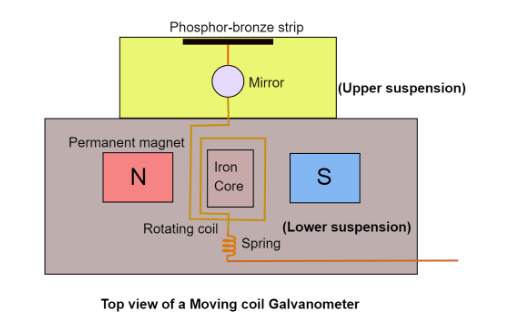
A moving coil galvanometer consists of a rectangular coil that is wound around a non-conductive material. This material also encloses a cylindrical soft iron core. The coil is suspended by a phosphor-bronze strip. It is surrounded by the opposite poles of two strong permanent magnets, which are concave shaped to allow the magnetic field lines to be as straight as possible, resulting in a uniform magnetic field.
The two terminals of the galvanometer are situated at the upper suspension (near the phosphor-bronze suspension wire) and the lower suspension (below the spring).
A concave mirror is also attached to the upper suspension strip to note the deflection of the coil with a lamp and scale arrangement.
Let a current $ I $ flow through the coil of the galvanometer.
Due to this current, the coil experiences a torque and deflects by an angle $ \theta $ . Given by-
 $ {T_D} = NIAB\sin \theta $
Where $ N $ is the number of turns of the coil,
 $ A $ is the area of the rectangular coil,
 $ B $ is the magnetic field of permanent magnets,
And $ \theta $ is the angle between the normal to the plane of rectangular coil and the Magnetic field lines.
This angle is equal to $ {90^\circ } $ .
 Thus the deflection torque becomes,
 $ {T_D} = NIAB $
 This also causes a restoring torque to develop in the suspension wire.
Let $ k $ be the rotating torque per unit angle per unit twist of the bronze strip, then the restoring torque applied by the strip is given by,
 $ {T_R} = k\theta $
Assuming that the deflection torque and the restoring torque are equal,
We can write-
 $ NIAB = k\theta $
Rearranging,
 $ I = \dfrac{{k\theta }}{{NAB}} $
We know that the quantities $ k,N,A,B\; $ are constant for a given galvanometer, thus they can be replaced with a single constant.
Let that constant be, $ G $ .
Then,
 $ I = G\theta $
The constant $ G $ is called the galvanometer constant.
Therefore,
 $ I \propto \theta $
Hence it is proved that the current passing through the galvanometer coil is directly proportional to the deflection caused in it.

Note:
Phosphor bronze is used in the construction of a moving coil galvanometer because it has small restoring torque per unit of twist. The coil is wound on a non-metallic frame because a metallic frame can produce eddy currents around the coil and give an inaccurate reading.