
Draw a pair of directed segments \[\overrightarrow{AB\text{ }}\text{and }\overrightarrow{XY}\] which are parallel, in the opposite sense, and equal in length. Find a directed segment which represents their sum. What can you say about (its length, (i) its direction ?)
Answer
590.4k+ views
Hint: Two parallel directed segments having same length but opposite direction.
Any two vectors that are parallel to each other can either be following in the same direction or in the opposite direction.
Complete step by step answer:
1) If the parallel vectors are opposite to each other, (i.e. at \[{{180}^{\circ }}\] with each other), then the magnitude of resultant is the difference of the magnitudes of the two.
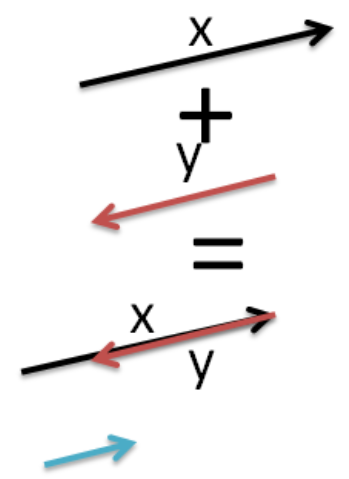
The direction is the same as that vector whose magnitude is the greatest among the two.
2) If both the vectors are in the same direction (at \[{{0}^{\circ }}\] with each other), the magnitude of resultant is just the simple addition of the magnitudes of the given vectors.
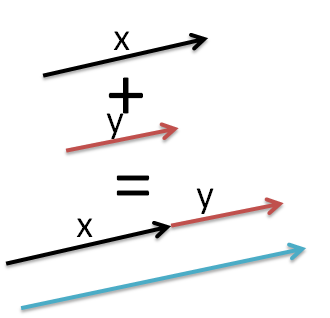
But this is not the case here. Here the vectors are opposite in a sense that means they are opposite in direction. Moreover their lengths are the same, which means they have the same magnitude.
Two vectors are equal if they have the same length (magnitude) and direction.
The sum of two vectors is their resultant. But here these two vectors are parallel. Moreover they are also opposite to each other so we need to find the difference between them.
So, we draw two directed segments \[\overrightarrow{AB\text{ }}\text{and }\overrightarrow{XY}\].
Thus the diagram will be somewhat similar to….
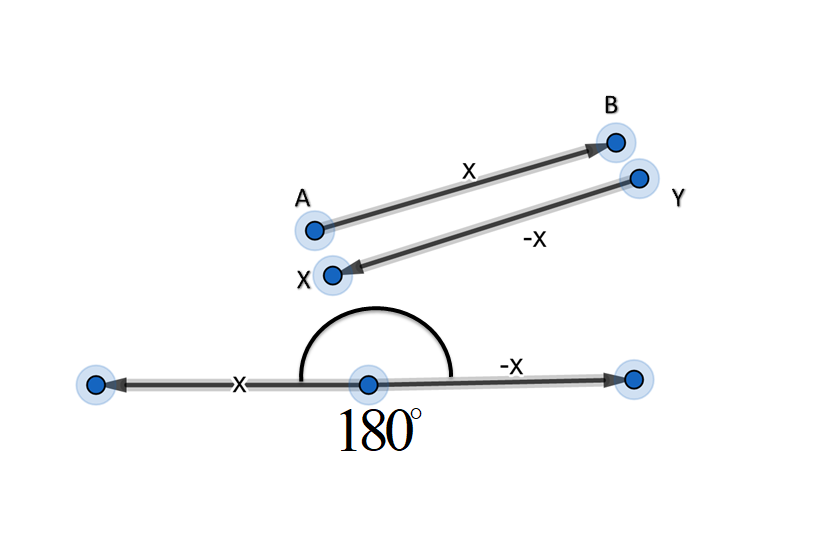
Having no new vector representing the sum of these two parallel vectors with the same magnitude but different direction.
Note: Since the magnitude of both the parallel vectors are the same when we are made to find a vector representing the sum of these two vectors we see that there is no sum. Since their magnitudes are the same their difference in magnitude becomes zero.
Their lengths are the same which signifies that their magnitude is the same. Their direction is opposite (opposite senses) so we find the difference of their magnitudes.
Any two vectors that are parallel to each other can either be following in the same direction or in the opposite direction.
Complete step by step answer:
1) If the parallel vectors are opposite to each other, (i.e. at \[{{180}^{\circ }}\] with each other), then the magnitude of resultant is the difference of the magnitudes of the two.
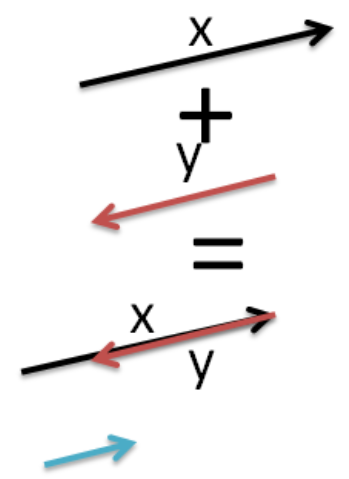
The direction is the same as that vector whose magnitude is the greatest among the two.
2) If both the vectors are in the same direction (at \[{{0}^{\circ }}\] with each other), the magnitude of resultant is just the simple addition of the magnitudes of the given vectors.

But this is not the case here. Here the vectors are opposite in a sense that means they are opposite in direction. Moreover their lengths are the same, which means they have the same magnitude.
Two vectors are equal if they have the same length (magnitude) and direction.
The sum of two vectors is their resultant. But here these two vectors are parallel. Moreover they are also opposite to each other so we need to find the difference between them.
So, we draw two directed segments \[\overrightarrow{AB\text{ }}\text{and }\overrightarrow{XY}\].
Thus the diagram will be somewhat similar to….

Having no new vector representing the sum of these two parallel vectors with the same magnitude but different direction.
Note: Since the magnitude of both the parallel vectors are the same when we are made to find a vector representing the sum of these two vectors we see that there is no sum. Since their magnitudes are the same their difference in magnitude becomes zero.
Their lengths are the same which signifies that their magnitude is the same. Their direction is opposite (opposite senses) so we find the difference of their magnitudes.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




