Question

How to draw a pair of tangents to a circle of radius 5cm which are inclined to the angle of \[{{60}^{0}}\] ?

Answer 1

Hint: In order to draw a pair of tangent, it is given that angle between the tangents is \[{{60}^{0}}\] then we will get to know that the angle at the centre is \[{{120}^{0}}\] using the tangent property of circles. then we just need to draw the figure according to the measures of angles and the radius and you will end up to getting the required figure i.e. a figure of a pair of tangent to a circle of radius 5cm which are inclined to the angle of \[{{60}^{0}}\] .

Complete step-by-step answer:
We have given that,
The measure of angle between the tangents is \[{{60}^{0}}\] .
Since, we know the property of a circle which states that the angle at center is double the measure of angle between the tangents.
Angle between the tangent = \[{{60}^{0}}\]
Therefore,
Angle at the centre = \[2\times {{60}^{0}}={{120}^{0}}\]
Also,
The tangent to the circle is perpendicular to the radius.
Thus,
We draw a circle of radius 5 cm, then draw a radius, then will draw the second radius at \[{{120}^{0}}\] from the first radius.
Then draw a perpendicular from both the radius using the protractor.
The figure is as follows;

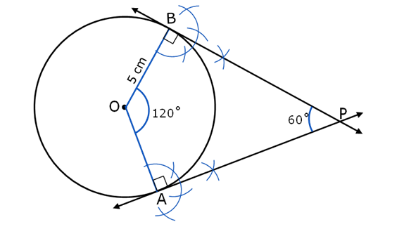
Hence, it is the required figure.



Note: In order to draw a figure of the given question, students need to remember the tangent property of the circle which states that the angle at the centre of the circle is double the angle between the tangents. They should also know that the tangents are always perpendicular to radius. If the students do not know about these properties they will end up drawing the wrong figure. Here, in the above question, we can also draw an angle using D also if you don’t know to draw an angle using a protractor.