
Draw a right triangle ABC in which
Answer
471.3k+ views
Hint: We start solving the problem by first drawing the line segment AB and then drawing an arc of length 8 cm taking B as centre. We then construct angle
Complete step by step answer:
According to the problem, we are asked to construct a triangle with measurements
The following are the steps to construct the given figures.
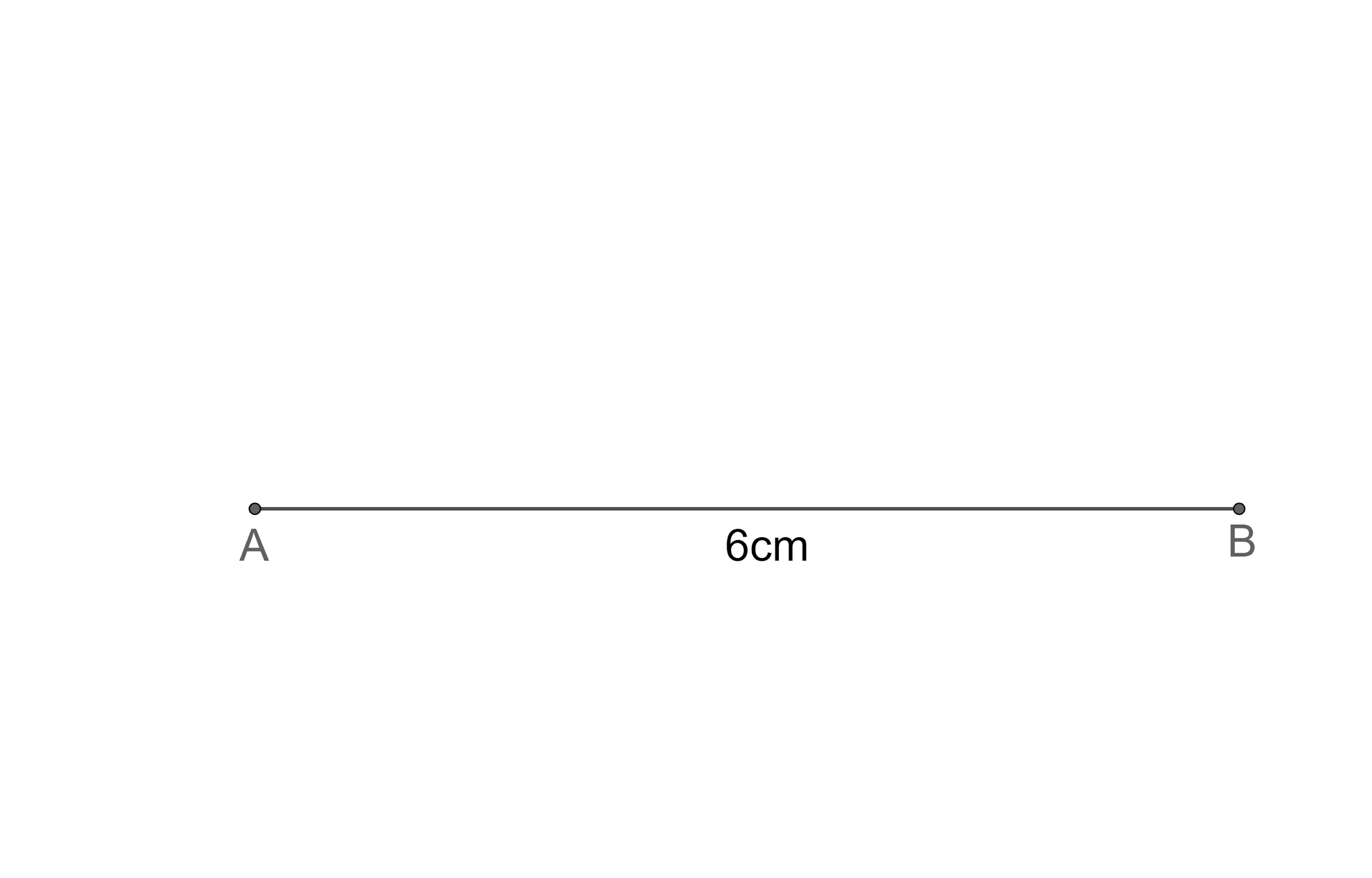
Step1: Let us first draw the line segment AB of length 6 cm.
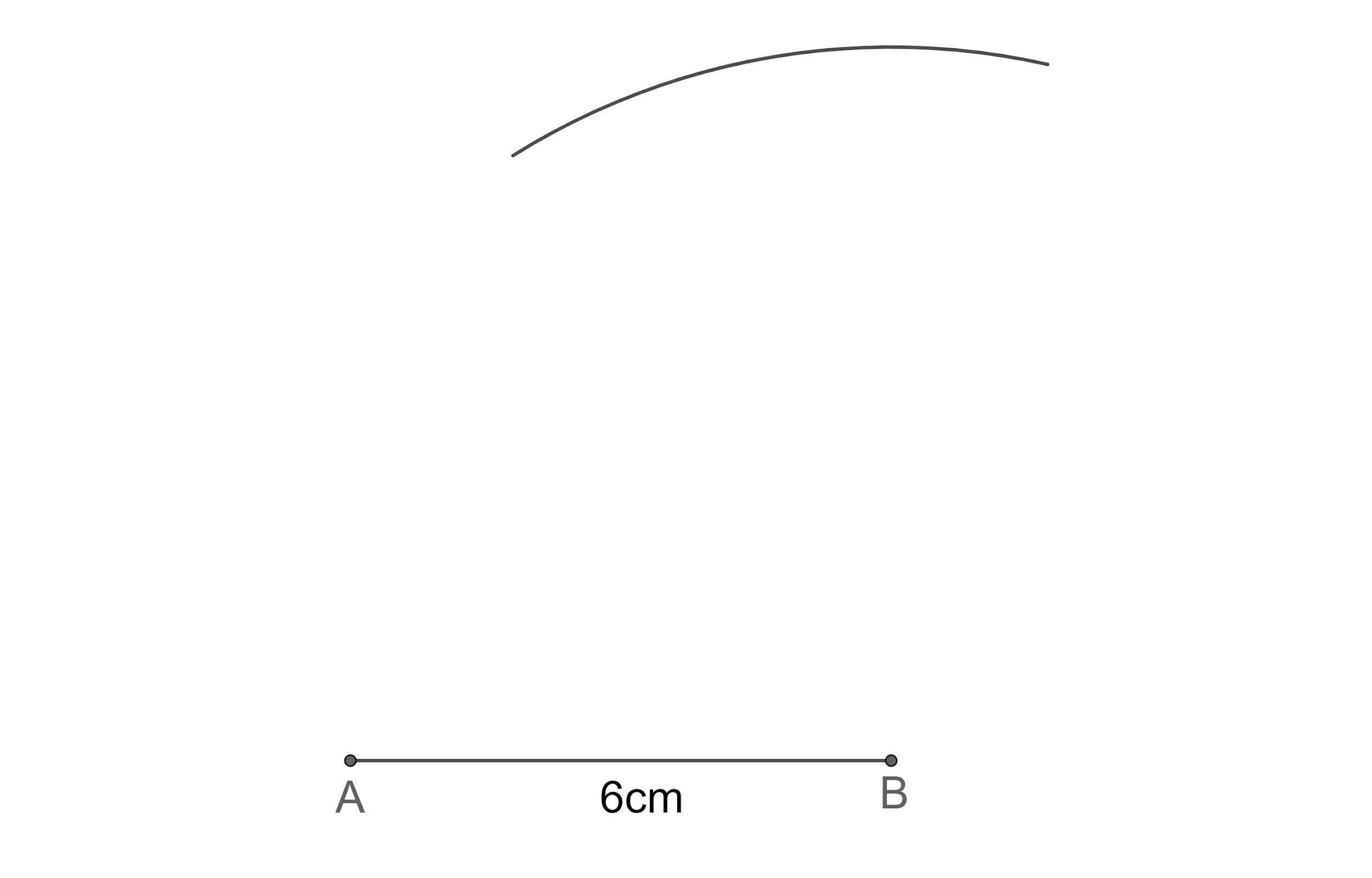
Step 2: Now, we draw an arc of radius 8 cm taking B as a centre.
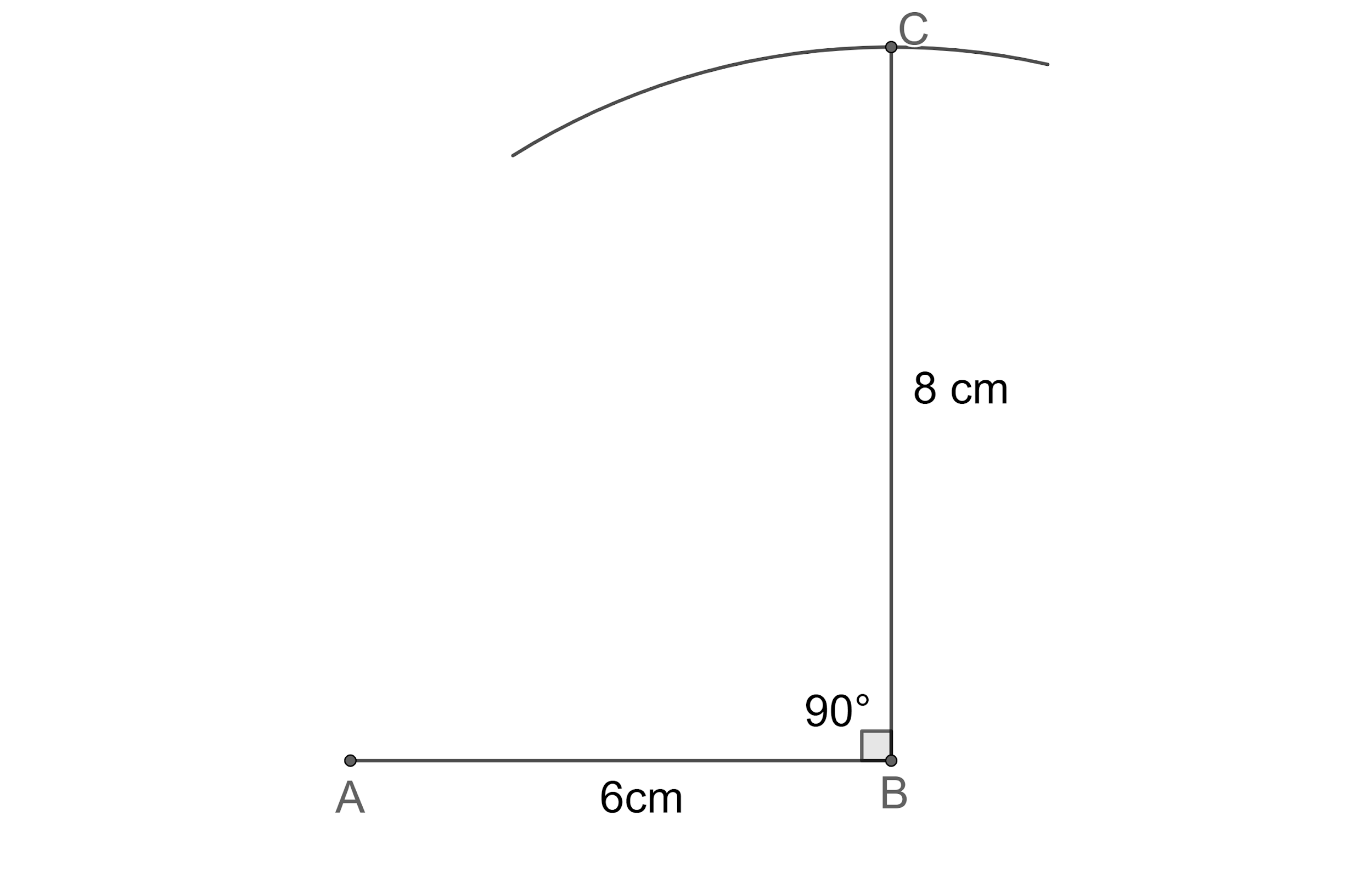
Step 3: Now, let us construct angle
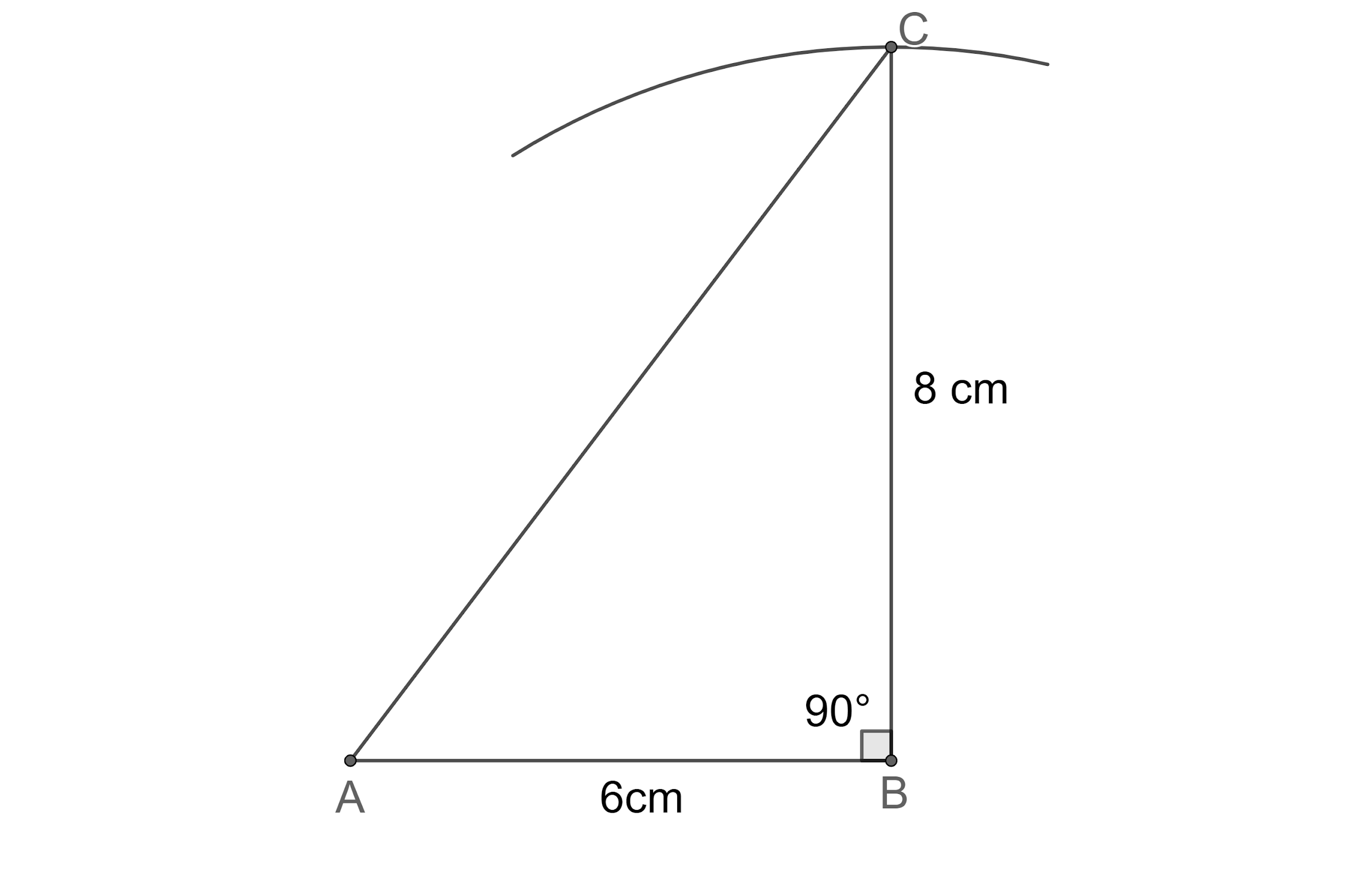
Step 4: Now, let us join the points A and C to complete the construction of triangle ABC.
Step 5: Now, let us draw an arc of any radius less than the length of side AC taking B as centre intersecting the side AC at two points E and F.
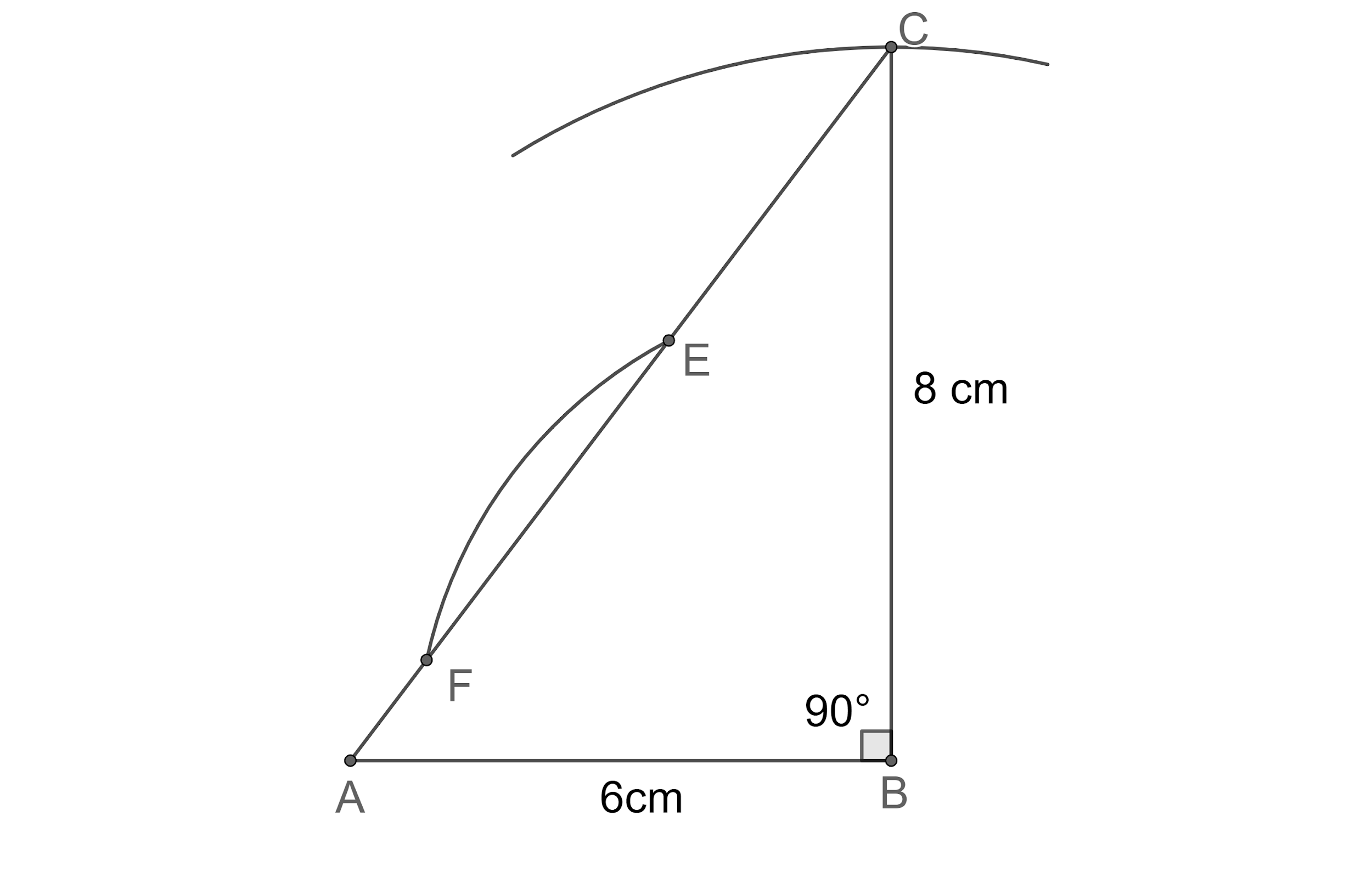
Step 6. Now, let us draw an arc of the radius of 1 cm taking F as centre outside the triangle.
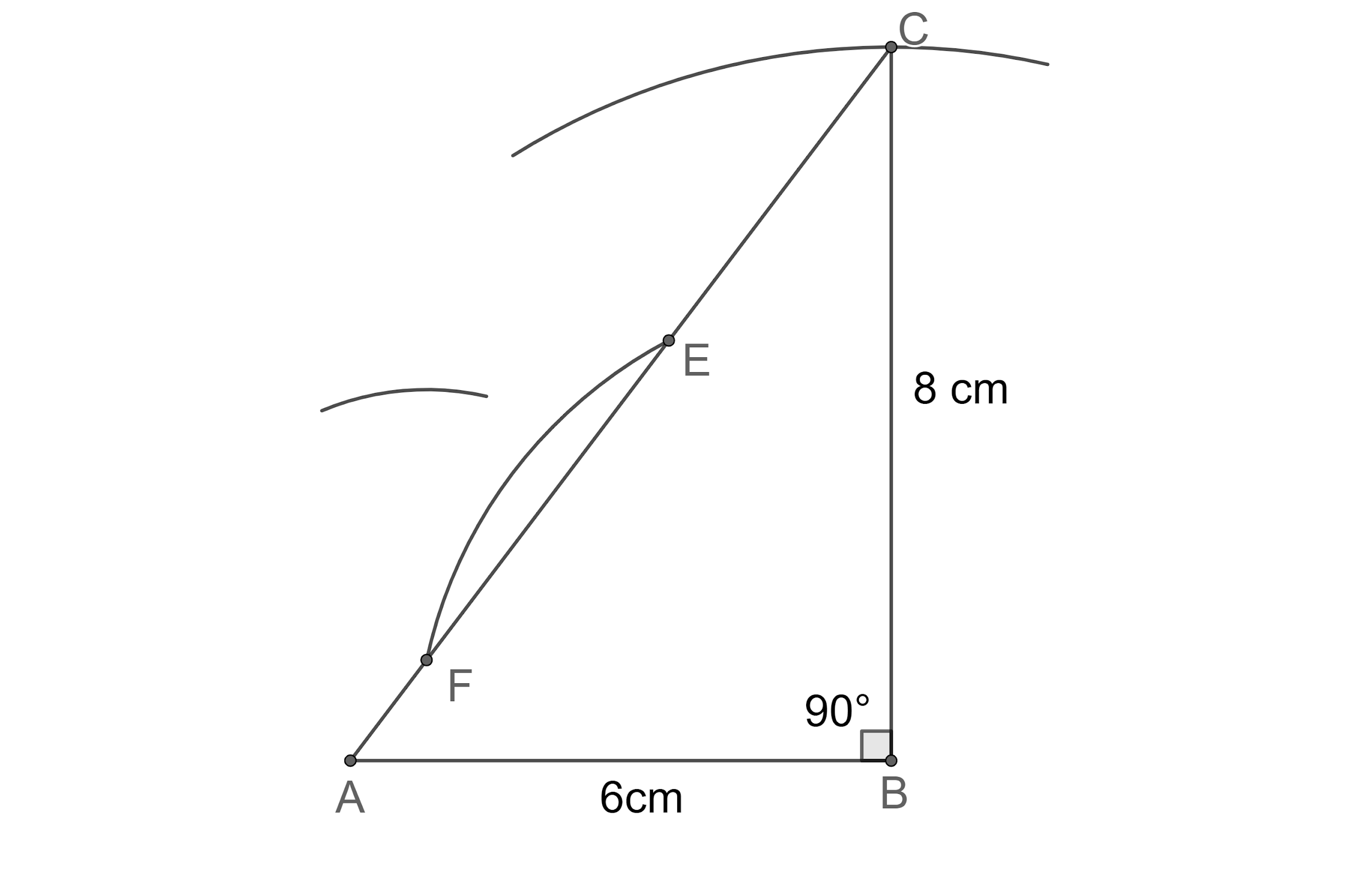
Step 7: Now, let us draw an arc of the radius of 1 cm taking E as centre outside the triangle, which intersects the other arc at point O.
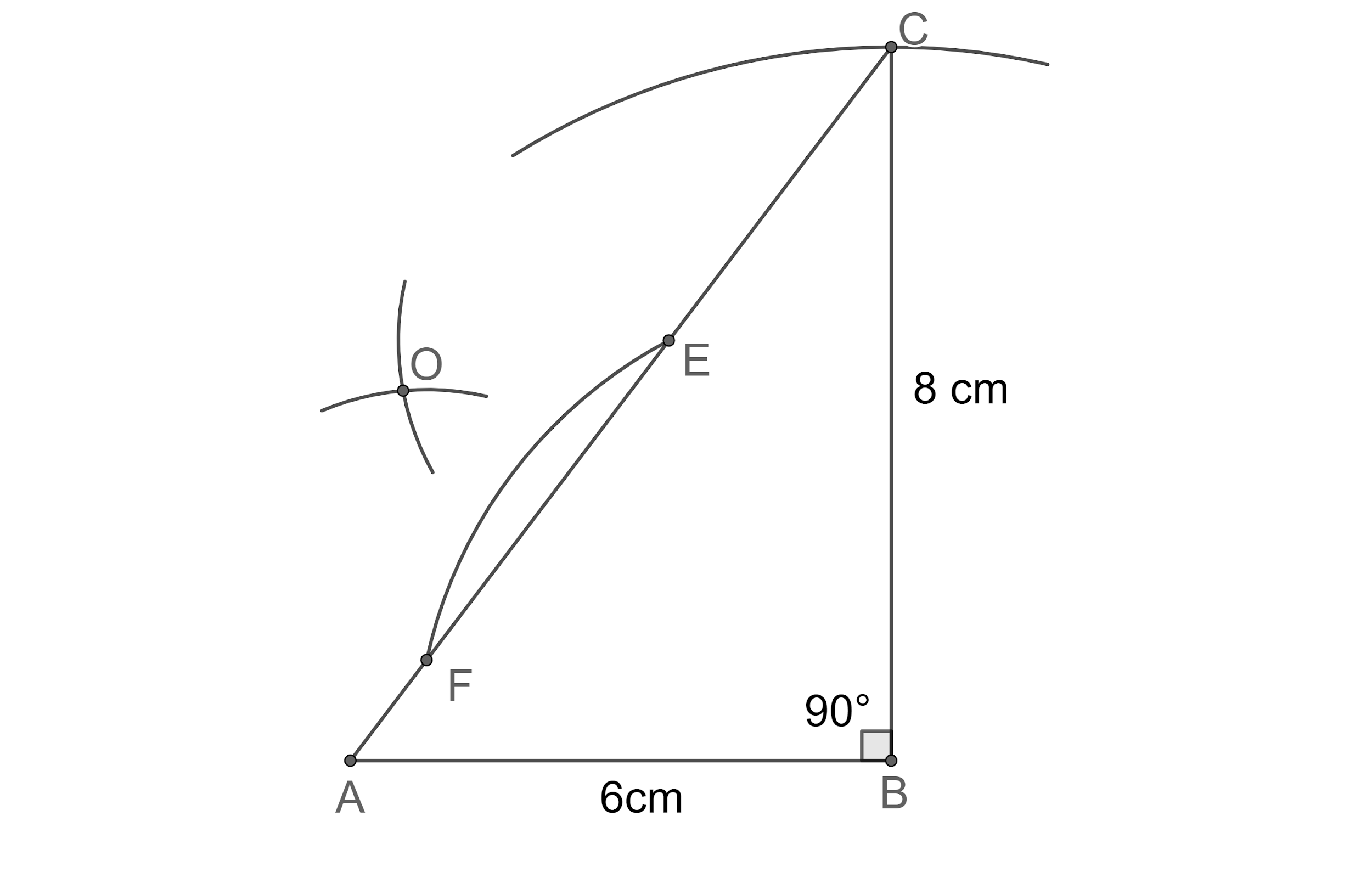
Step 8: Now, let us join the points O and B, which intersects side AC at D.
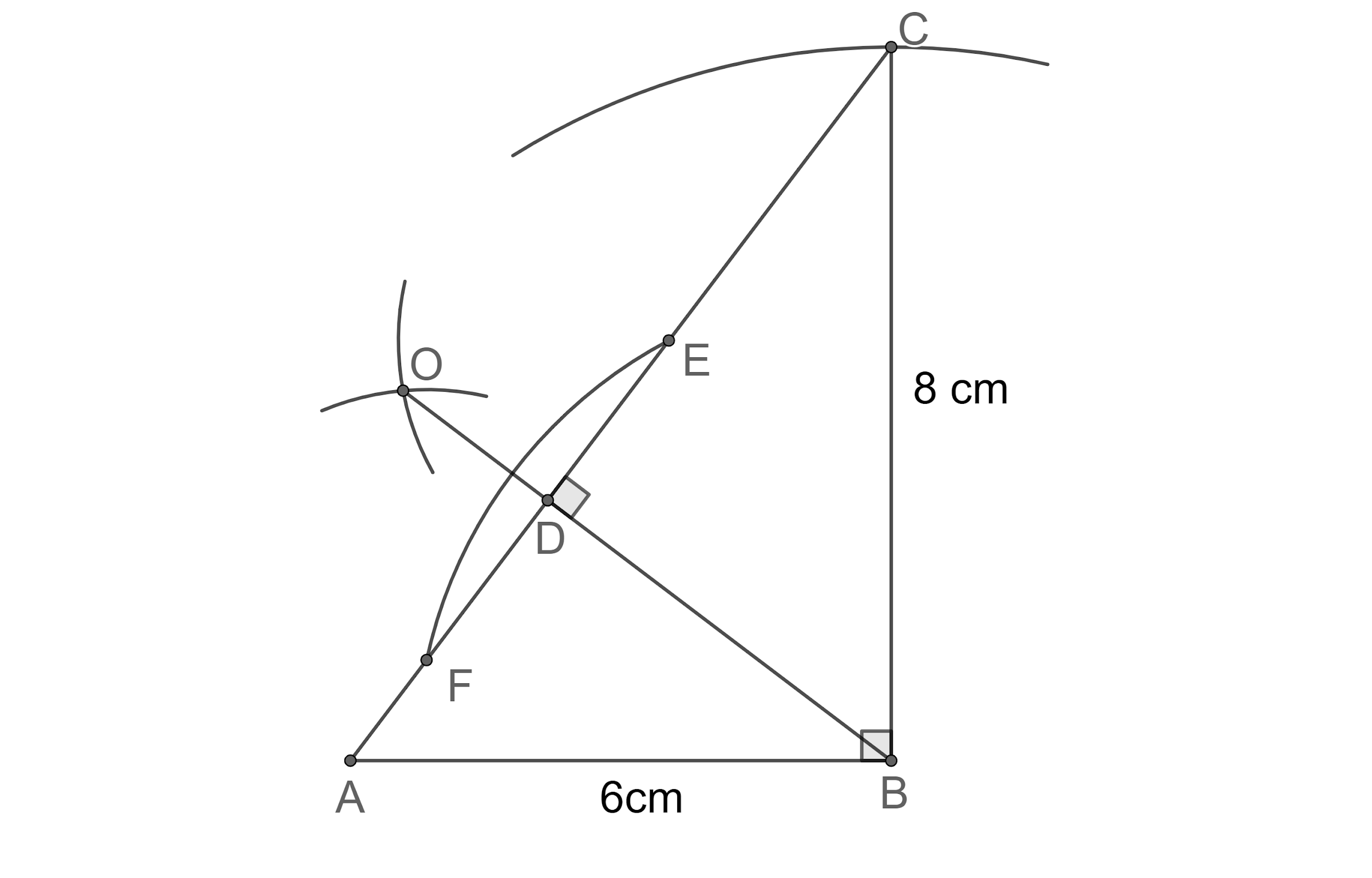
Step 9: Now, let us draw an arc of the radius of 5 cm taking B as centre.
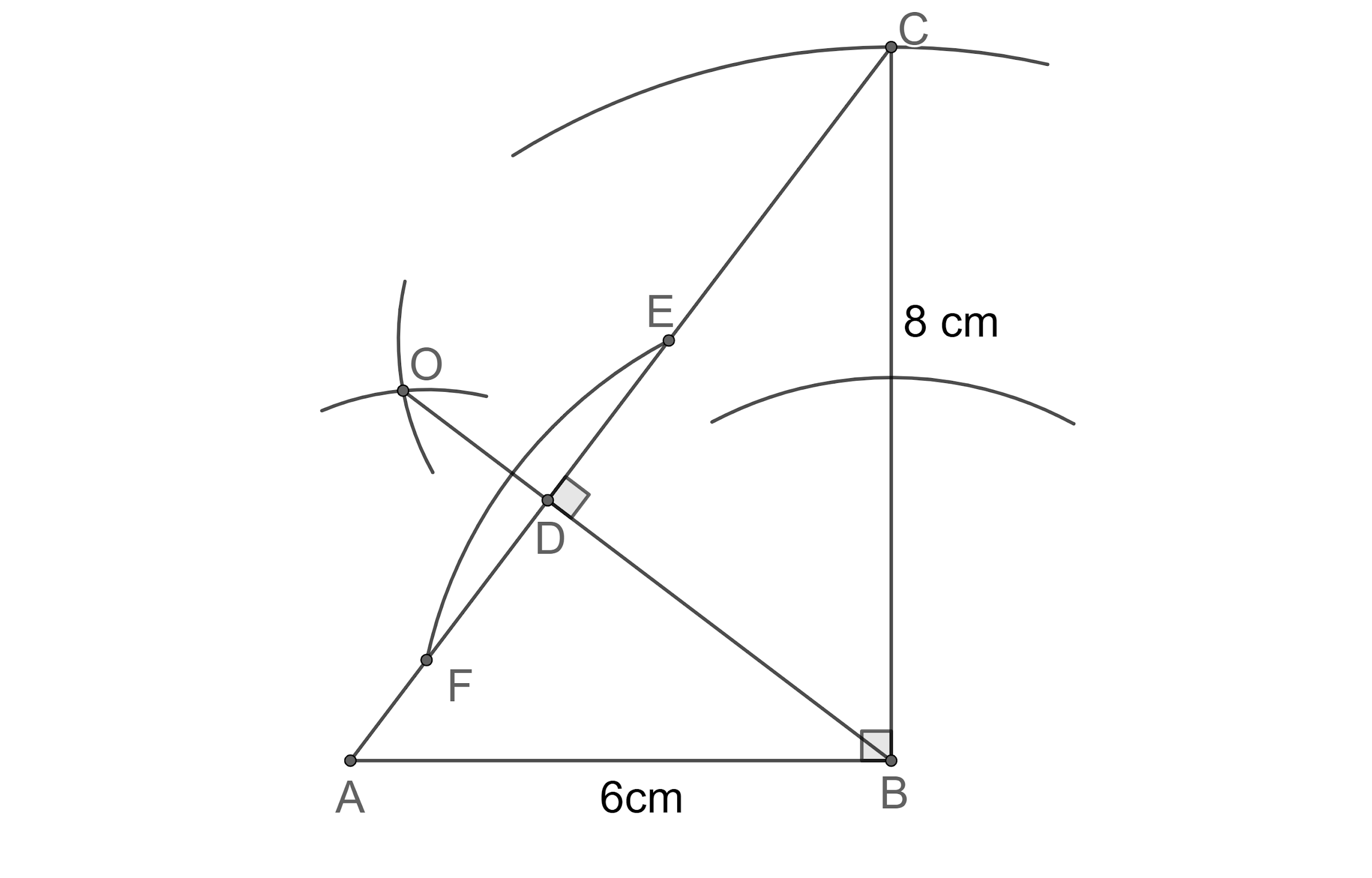
Step 9: Now, let us draw an arc of radius of 5 cm taking C as centre intersecting the previous arc at R and T.
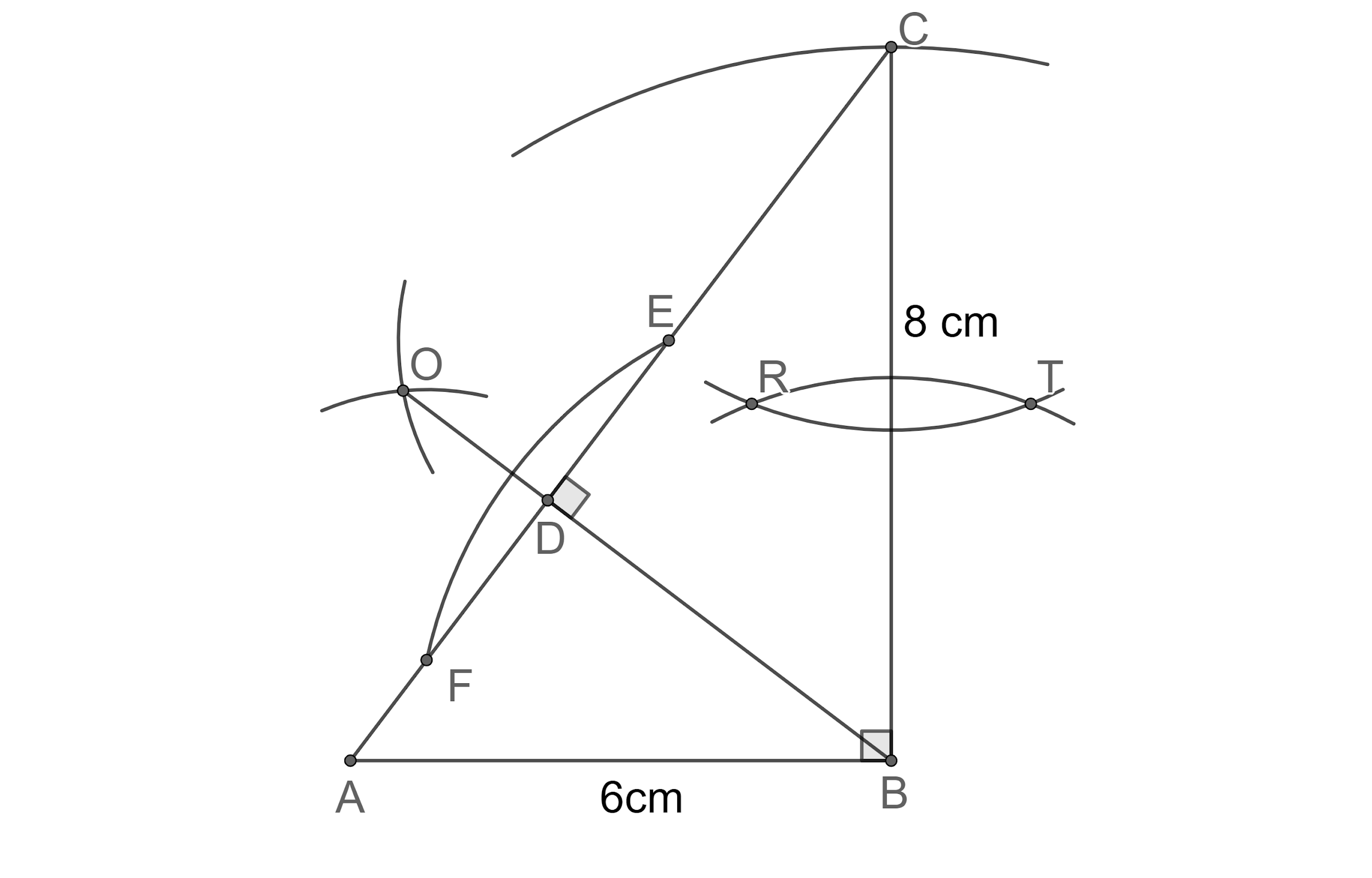
Step 10: Now, let us join the points R and T which intersects side BC at S, which is the circumcentre of the triangle BDC.
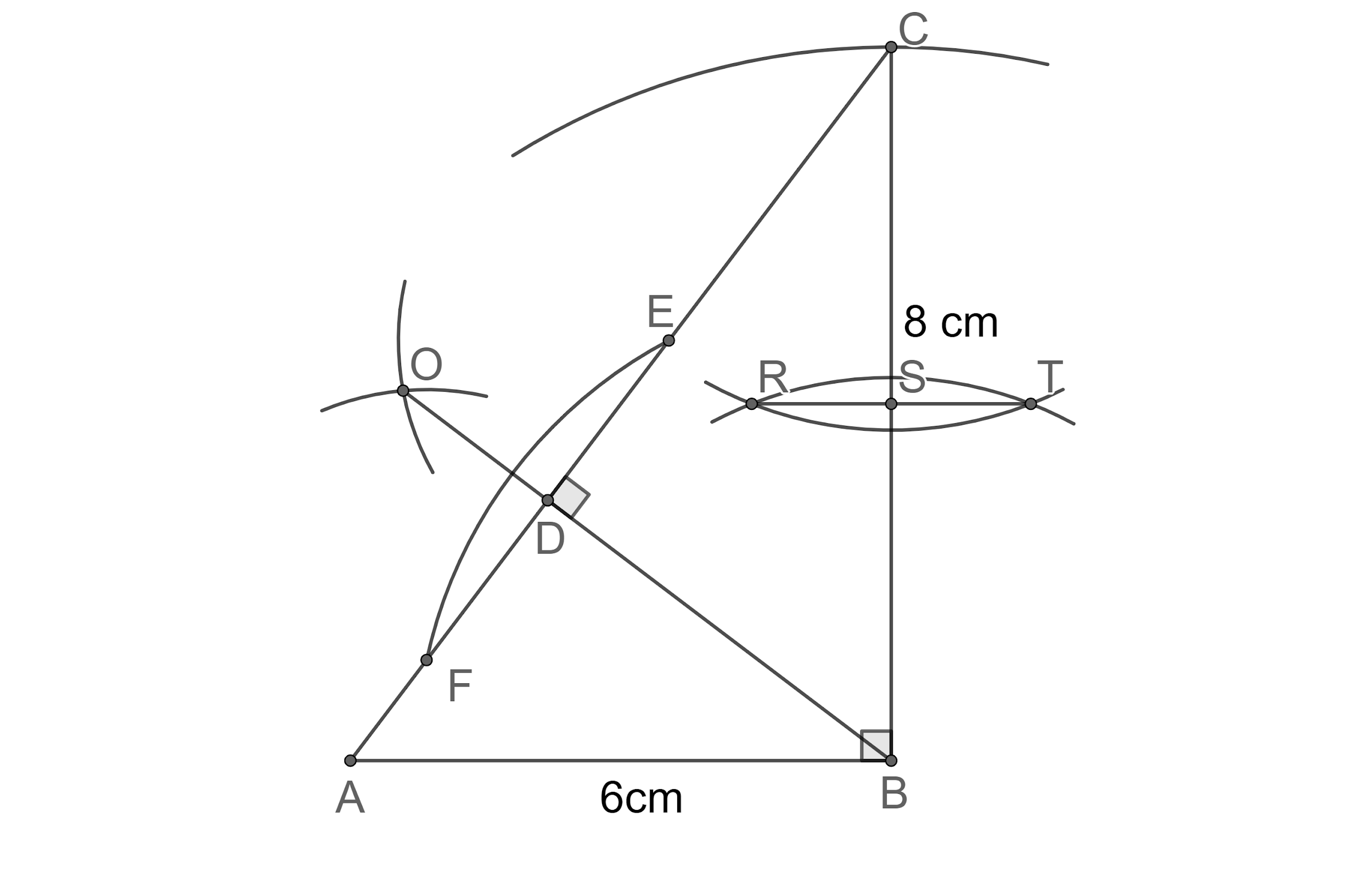
Step 11: Let us draw a circle passing through points D, C and B taking S as centre.
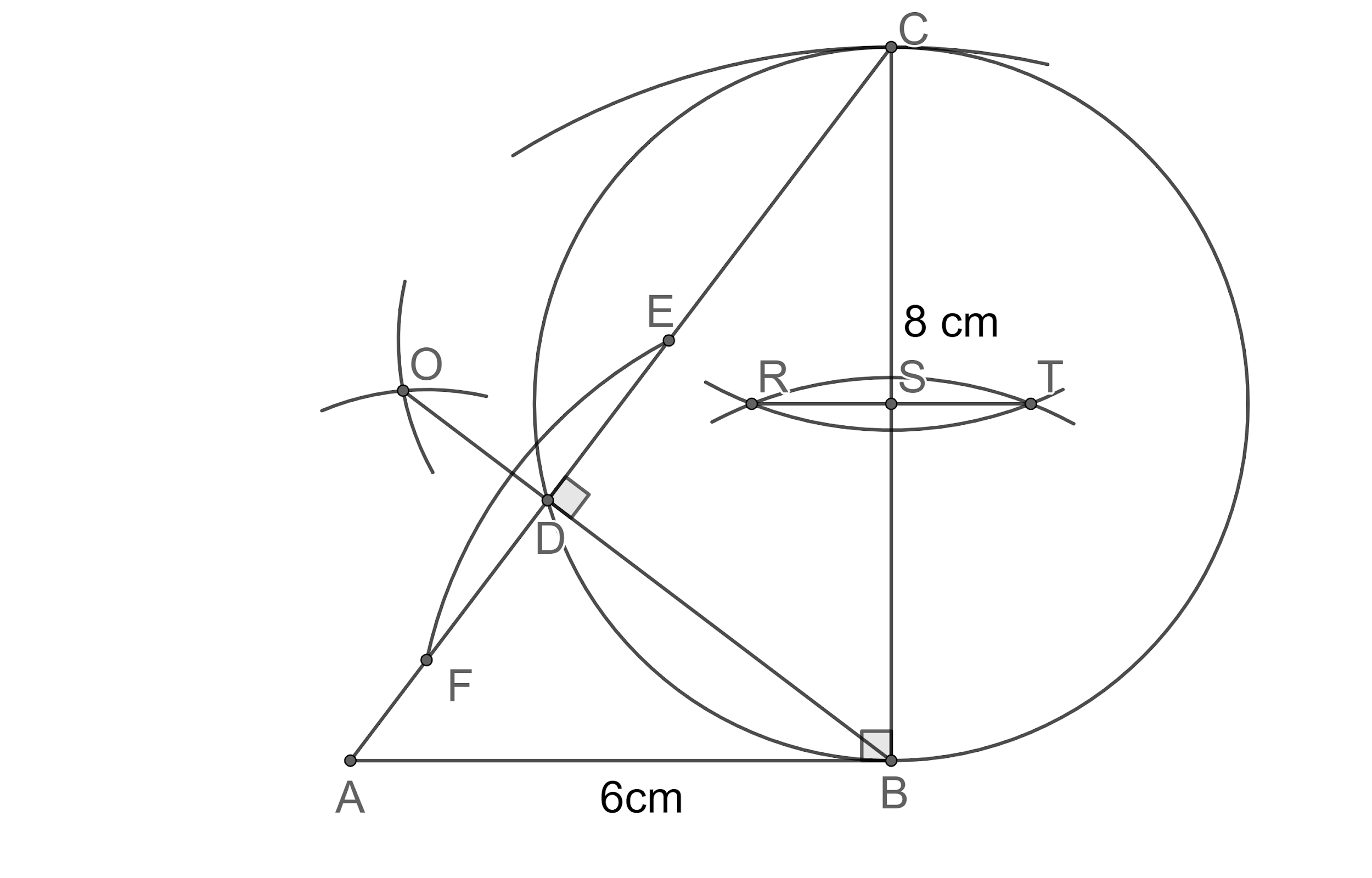
Step 12: Now, let us joint the points A and S.
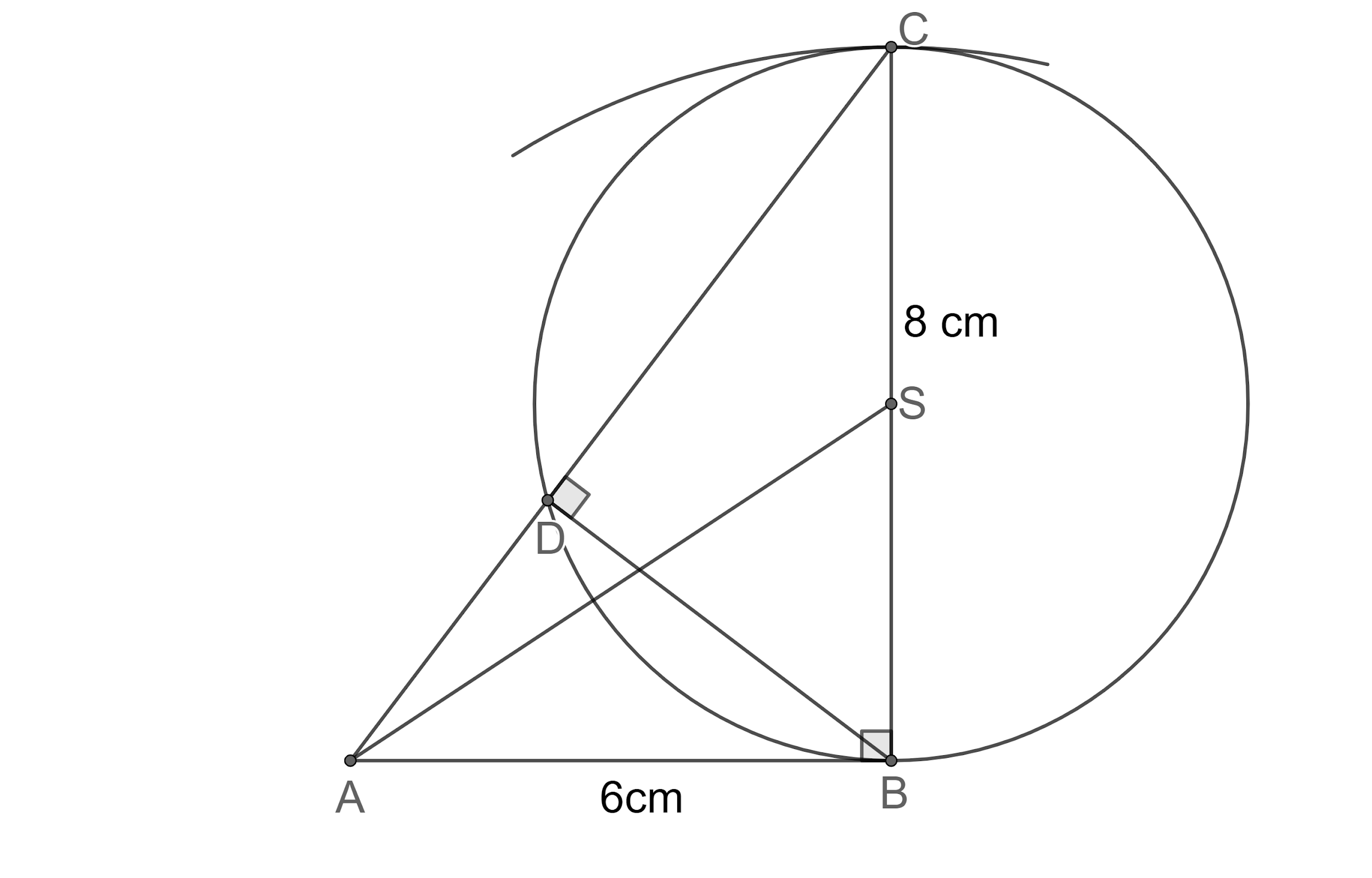
Step 13: Now, let us draw arcs of a radius of 5 cm taking A as centre as shown below:
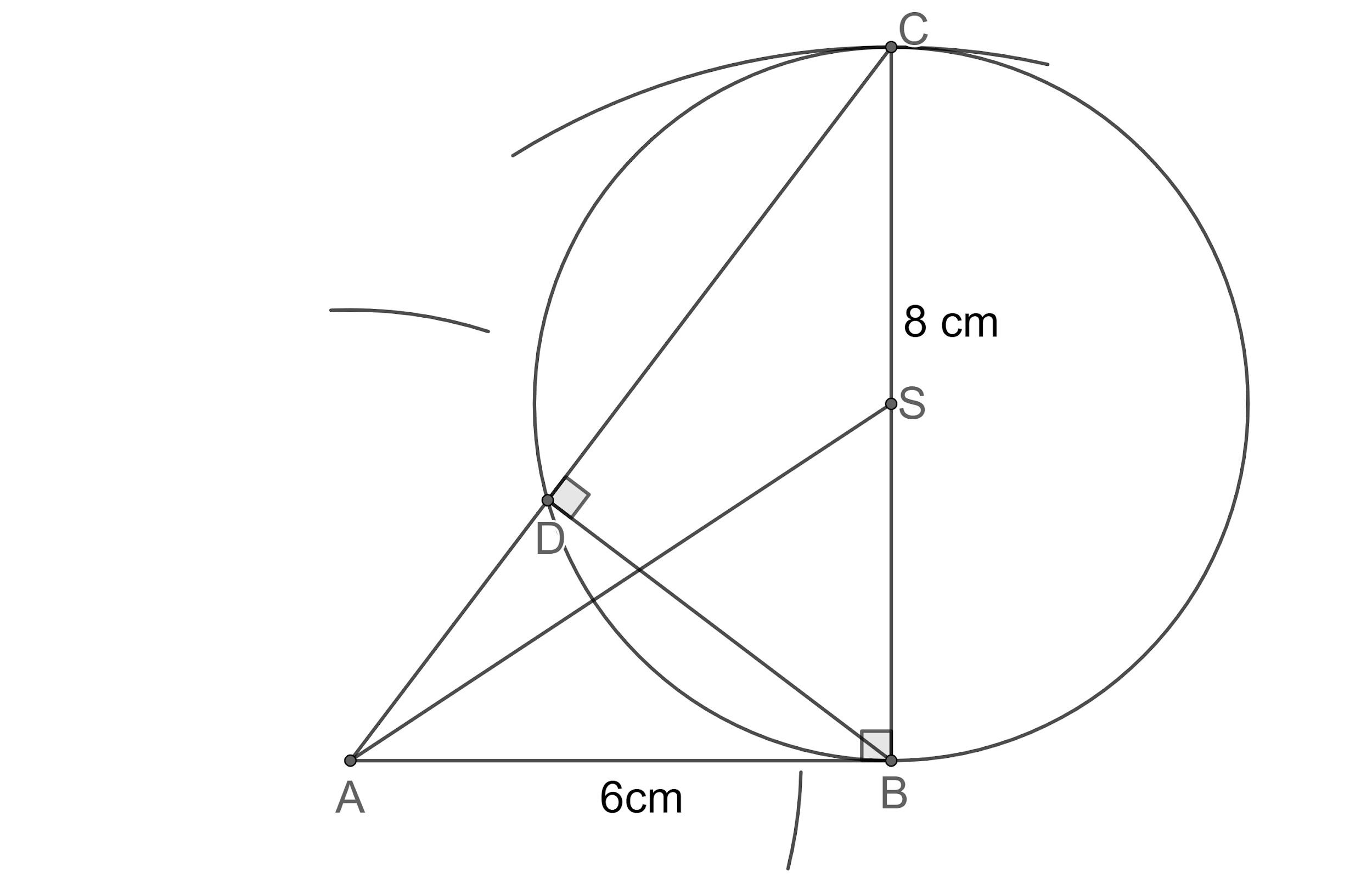
Step 14: Now, let us draw arcs of the radius of 5 cm taking S as centre as shown below insecting the previous arcs at U and V:
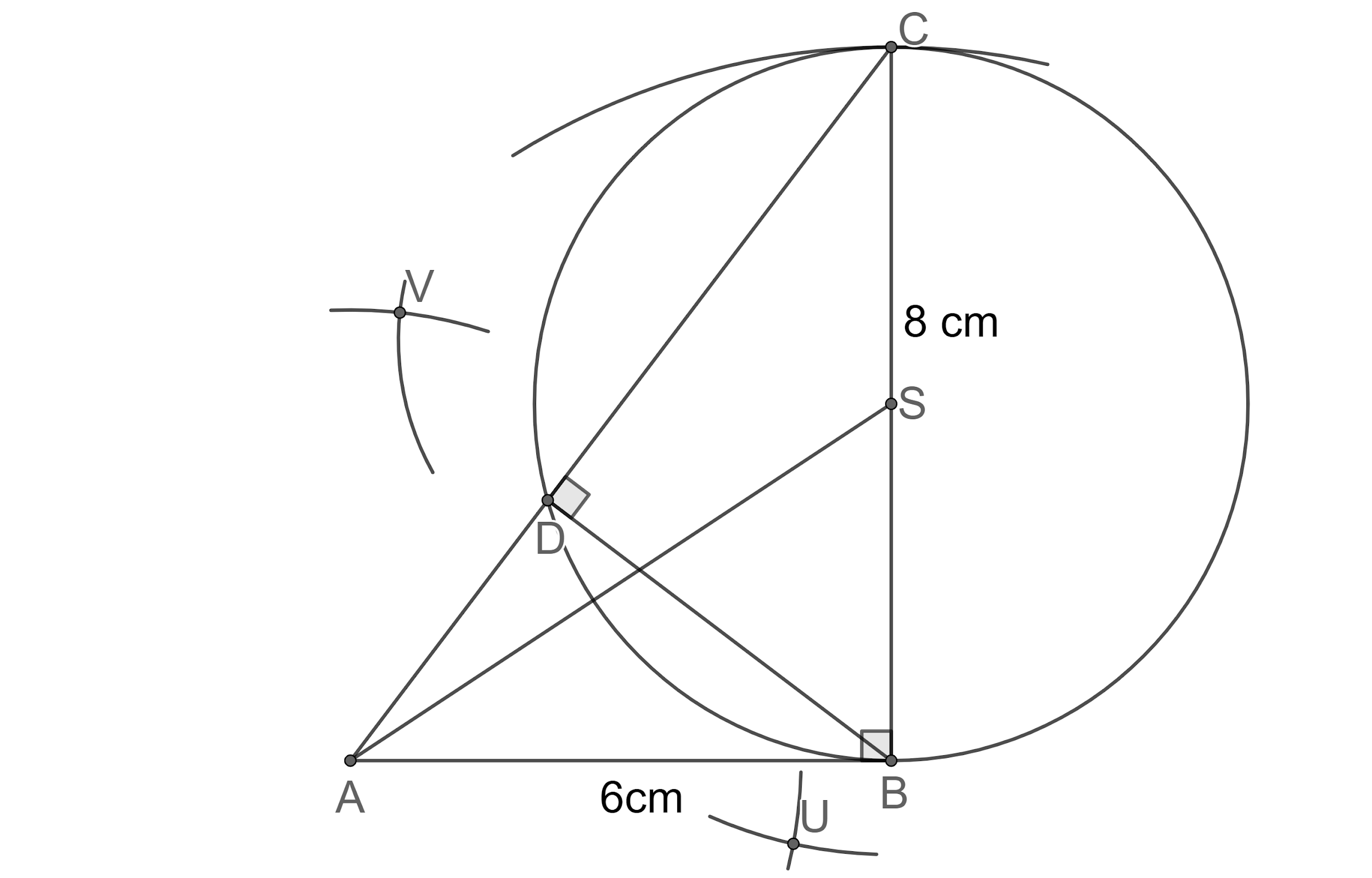
Step 15: Now, let us join the points R and T which intersects AS at W.
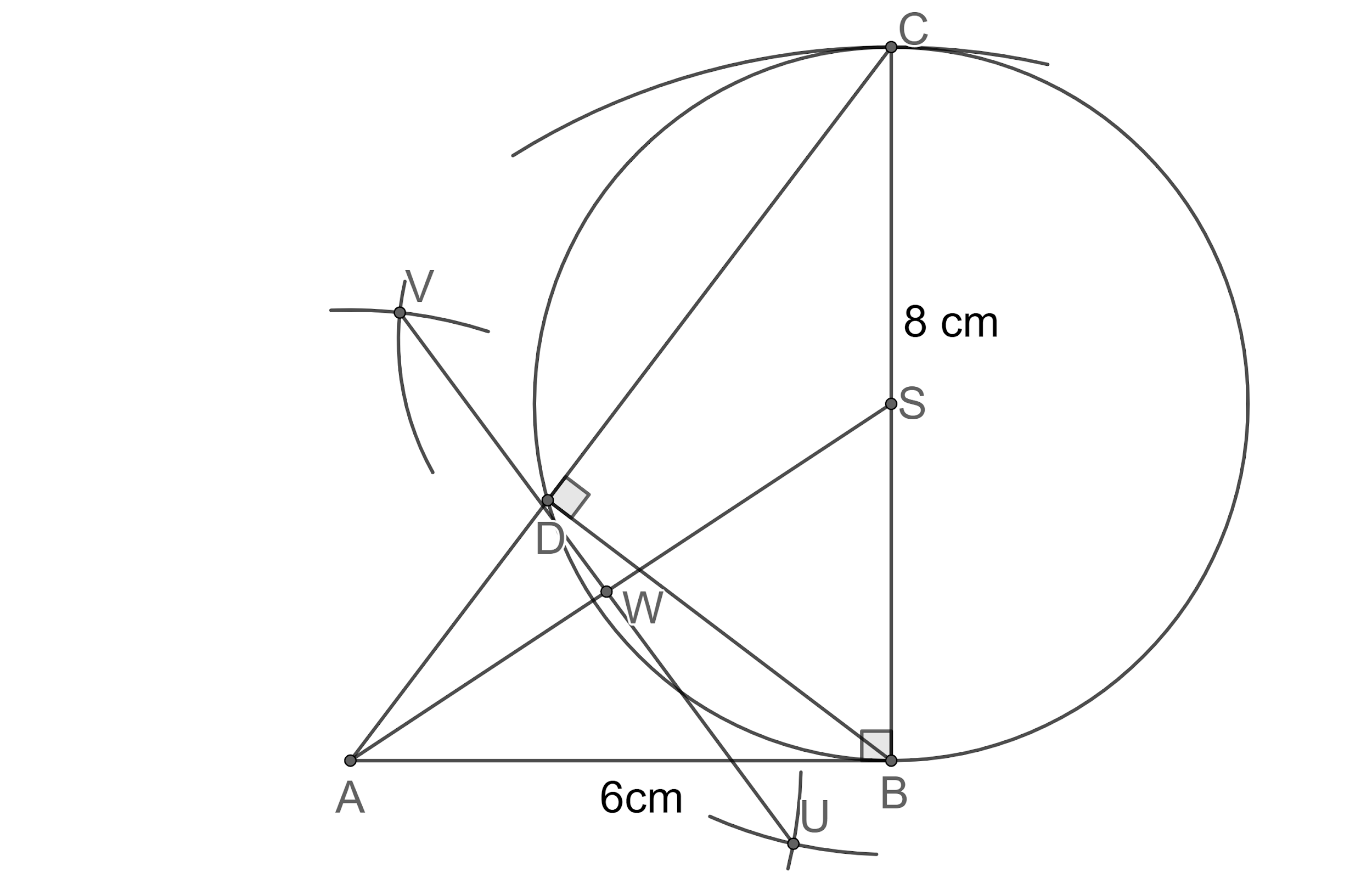
Step 16: Now, let us draw arcs of length AW taking W as centre intersecting the circle at points X and B.
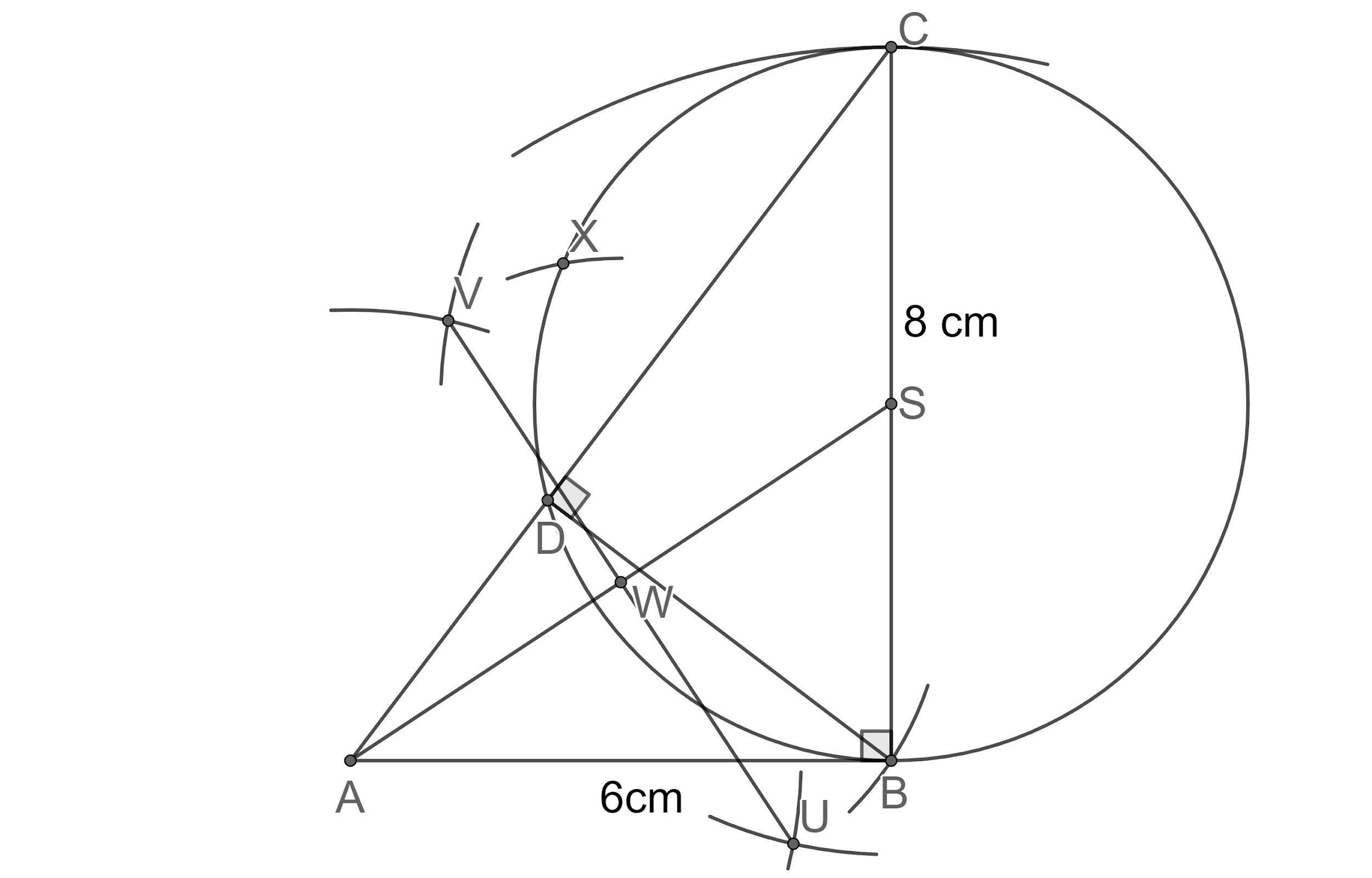
Step 17: Now, let us join points A and X, A and B to construct the required tangents.
Note:
We should perform each step carefully to avoid confusion while constructing the triangles and tangents. We should know that the circumcentre lies on the mid-point of the hypotenuse in a right-angle triangle. We should keep in mind that the BD is the altitude of the triangle, not the perpendicular bisector as perpendicular bisectors need to pass through the vertex in a triangle. Similarly, we can expect problems to construct the incircle of the triangle BDC.
Complete step by step answer:
According to the problem, we are asked to construct a triangle with measurements
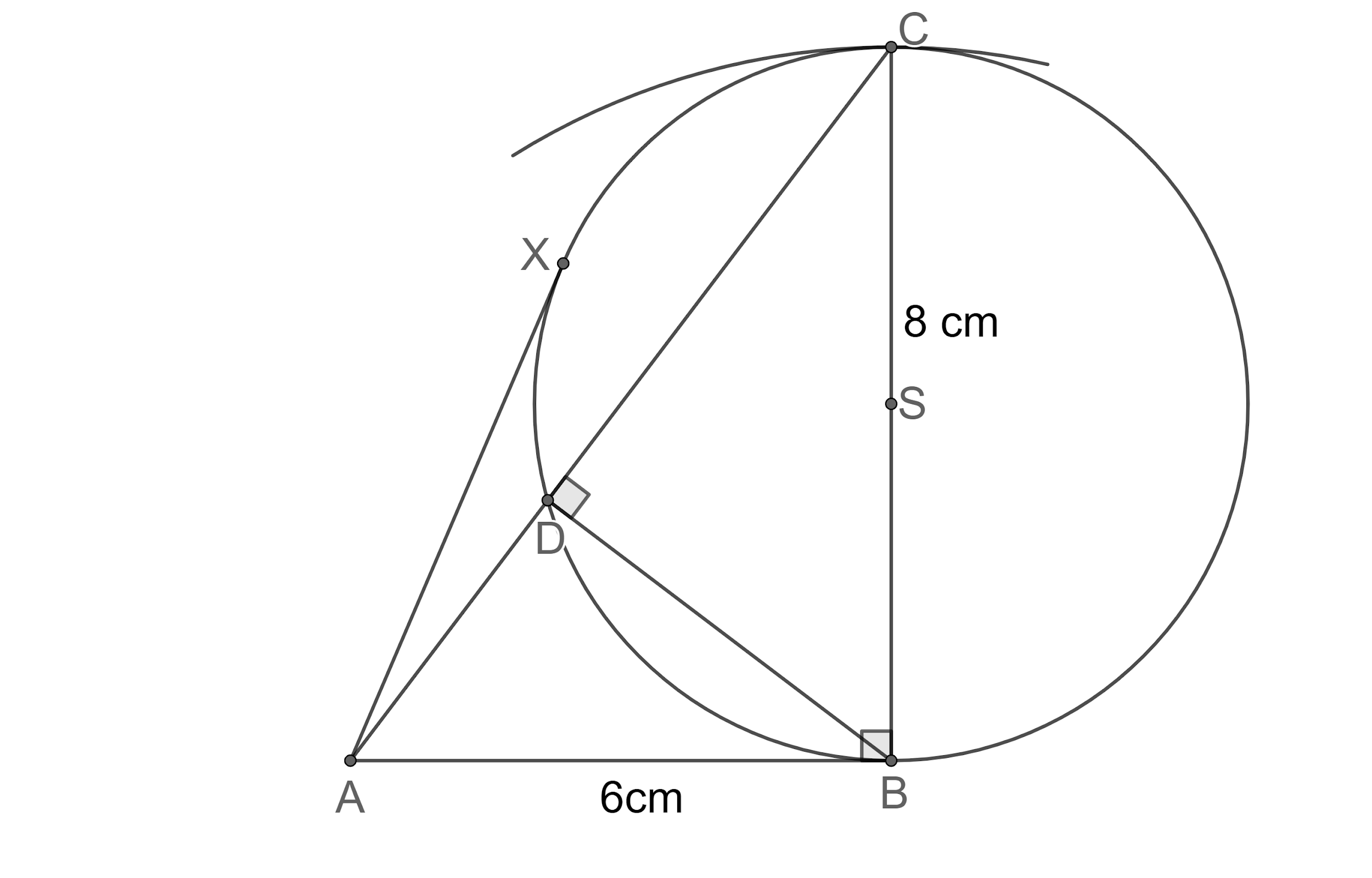
The following are the steps to construct the given figures.
Step1: Let us first draw the line segment AB of length 6 cm.

Step 2: Now, we draw an arc of radius 8 cm taking B as a centre.

Step 3: Now, let us construct angle

Step 4: Now, let us join the points A and C to complete the construction of triangle ABC.

Step 5: Now, let us draw an arc of any radius less than the length of side AC taking B as centre intersecting the side AC at two points E and F.

Step 6. Now, let us draw an arc of the radius of 1 cm taking F as centre outside the triangle.

Step 7: Now, let us draw an arc of the radius of 1 cm taking E as centre outside the triangle, which intersects the other arc at point O.

Step 8: Now, let us join the points O and B, which intersects side AC at D.

Step 9: Now, let us draw an arc of the radius of 5 cm taking B as centre.

Step 9: Now, let us draw an arc of radius of 5 cm taking C as centre intersecting the previous arc at R and T.

Step 10: Now, let us join the points R and T which intersects side BC at S, which is the circumcentre of the triangle BDC.

Step 11: Let us draw a circle passing through points D, C and B taking S as centre.

Step 12: Now, let us joint the points A and S.

Step 13: Now, let us draw arcs of a radius of 5 cm taking A as centre as shown below:

Step 14: Now, let us draw arcs of the radius of 5 cm taking S as centre as shown below insecting the previous arcs at U and V:

Step 15: Now, let us join the points R and T which intersects AS at W.

Step 16: Now, let us draw arcs of length AW taking W as centre intersecting the circle at points X and B.

Step 17: Now, let us join points A and X, A and B to construct the required tangents.

Note:
We should perform each step carefully to avoid confusion while constructing the triangles and tangents. We should know that the circumcentre lies on the mid-point of the hypotenuse in a right-angle triangle. We should keep in mind that the BD is the altitude of the triangle, not the perpendicular bisector as perpendicular bisectors need to pass through the vertex in a triangle. Similarly, we can expect problems to construct the incircle of the triangle BDC.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




