Question

Draw a rough sketch of a quadrilateral ABCD and identify:\[\]
(I) Two pairs of opposite sides \[\]
(II) Two pairs of adjacent sides \[\]
(III) Two pairs of opposite angles\[\]

Answer 1

Hint: We draw the quadrilateral four sides and denote the four vertices as A, B, C, D. We find opposite sides by checking which pair of sides do not share any common vertex. We find adjacent sides checking which pair of sides that share a common vertex. We find the opposite angles by checking which pair of internal angles that do not share any common side. \[\]

Complete step by step answer:
We know that a quadrilateral is a closed curve which has four line segments called sides which are joined by four vertices. Let us draw a quadrilateral of our choice.\[\]
 

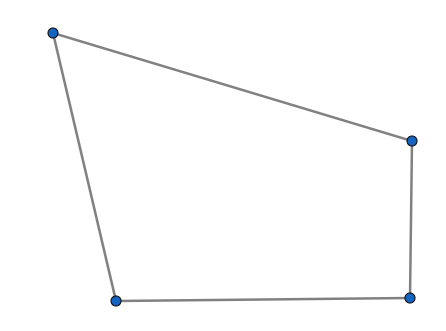
We start with naming any one of the four vertices as A. We can name the rest of the vertices B, C and D in clockwise or anti-clockwise direction. We denote the bottom left vertex as A and name the rest of the vertices B, C and D in an anti-clockwise direction. We have the figure as \[\]

The sides of the above sketched quadrilateral ABCD are
\[\text{AB,BC,CD,DA}\]
The internal angles of the quadrilateral ABCD are
\[\angle ABC.\angle BCD,\angle CDA,\angle DAB\]
(I) We know that two pairs of sides are called opposite sides in a quadrilateral if they do not have any common vertex. The pairs of sides that do not have common vertex are AB, CD and DA, BC. So the opposite sides are
\[\text{AB,}\text{CD and DA,BC}\]
(II) We know that two pairs of sides are called opposite sides in a quadrilateral if they have a common vertex. The pair of sides with common vertex B is AB, BC and the pair of sides with common vertex C is CD, DA. So the adjacent sides are
\[\text{AB,}\text{BC and DA,CD}\]
(III) We know that a pair internal angles are called opposite angles if they do not have any common side. The pairs of angles that do not have any common side are $\angle ABC,\angle CDA$ and $\angle BCD,\angle DAB$. So the opposite angles are
\[~\angle \text{ABC},\angle \text{CDA and }\angle \text{BCD},\angle \text{DAB}\]

Note: We note that pairs of internal angles are called adjacent angles if they do have a common side. If both pairs of opposite angles are equal then the quadrilateral is called parallelogram. If the both adjacent sides and opposite sides are equal then it is called a rhombus. We can also draw a convex quadrilateral with one reflex angle.