Question

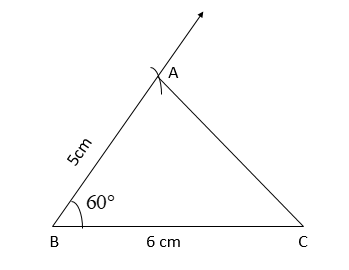
Draw a triangle \[ABC\] with side BC = 6 cm, AB = 5 cm and $\angle ABC = 60^\circ $. Then construct a triangle whose sides are $\dfrac{3}{4}$ of the corresponding sides of the triangle \[ABC\].

Answer 1

Hint: Here, we first draw $\vartriangle ABC$ with such that base BC = 6 cm, AB = 5 cm, and $\angle ABC = 60^\circ $
Then we draw a ray BX below the triangle and mark points ${B_1},{B_2},{B_3},{B_4}$ on it such that$B{B_1} = {B_1}{B_2} = {B_2}{B_3} = {B_3}{B_4}$. After this step, we need to draw $A'C'\parallel AC$ and and ${B_3}C'||{B_4}C$ such that A’ and C’ are points on the sides AB and BC respectively. This gives us $\vartriangle A'BC'$ which is the required triangle.

Complete step-by-step answer:
We are given the lengths of the sides of a triangle \[ABC\]: BC = 6 cm, AB = 5 cm.
Also, we are given that $\angle ABC = 60^\circ $.
We are asked to construct this triangle and also a triangle whose sides are $\dfrac{3}{4}$ of the corresponding sides of $\vartriangle ABC$.
To construct triangle ABC:
1) Take BC as base.
2) Draw $\angle B = 60^\circ $. A ray originating from B and BC form arms of $\angle B$
3) Draw an arc of length 5 cm from point B on this ray.
4) This arc intersects at a point on the ray. Name it as A.
5) Draw segment AC to complete the triangle.

Now, to construct a triangle whose sides are $\dfrac{3}{4}$ of the corresponding sides of $\vartriangle ABC$, we follow the steps given below:
a) Draw a ray BX below the base BC such that $\angle CBX$forms an acute angle.
b) We will draw 4 small arcs from point B on ray BX and name the points of intersection of the arcs with the ray BX as ${B_1},{B_2},{B_3},{B_4}$ respectively such that $B{B_1} = {B_1}{B_2} = {B_2}{B_3} = {B_3}{B_4}$
c) Draw segment ${B_4}C$and segment ${B_3}C'$ such that ${B_3}C'||{B_4}C$.
We choose ${B_3}$ because ${B_3}$is the second point and the numerator of $\dfrac{3}{4}$ is 3.
d) Draw a line $A'C'$ parallel to $AC$ such that the line intersects side $AB$ at $A'$.

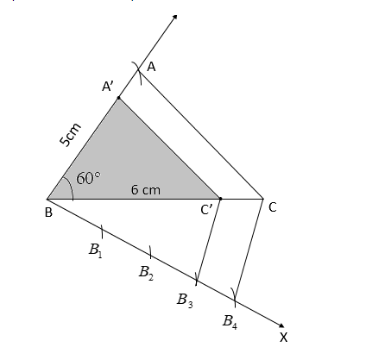
Then $\vartriangle A'BC'$ is the required triangle.
Now, we need to verify that the sides of $\vartriangle A'BC'$are $\dfrac{3}{4}$ of the corresponding sides of $\vartriangle ABC$.
That is we need to prove that \[\dfrac{{A'B}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{{BC'}}{{BC}} = \dfrac{3}{4}\]
We know that according to basic proportionality theorem, if a line parallel to one side of a triangle intersects the remaining two sides at two distinct points, then these two remaining sides are divided in equal ratio.
$
  {B_3}C'||{B_4}C \\
   \Rightarrow \dfrac{{B{B_3}}}{{{B_3}{{\rm B}_4}}} = \dfrac{{BC'}}{{C'C}} \\
 $
Now, $\dfrac{{B{B_3}}}{{{B_3}{{\rm B}_4}}} = \dfrac{3}{1}$
Therefore, we get
 \[
  \dfrac{{BC'}}{{C'C}} = \dfrac{3}{1} \\
   \Rightarrow \dfrac{{C'C}}{{BC'}} = \dfrac{1}{3} \\
 \]
We will add 1 on both the sides of the above equation and we get
\[
  \dfrac{{C'C}}{{BC'}} + 1 = \dfrac{1}{3} + 1 \\
   \Rightarrow \dfrac{{C'C + BC'}}{{BC'}} = \dfrac{4}{3} \\
   \Rightarrow \dfrac{{BC}}{{BC'}} = \dfrac{4}{3} \\
 \]
Let’s take reciprocal on both sides. Then we get
\[\dfrac{{BC'}}{{BC}} = \dfrac{3}{4}.....(1)\]
Consider $\vartriangle ABC$ and $\vartriangle A'BC'$
We have $\angle ABC \cong \angle A'BC'$ (common angles)
$\angle BC'A' \cong \angle BCA$($A'C'\parallel AC \Rightarrow $$\angle BC'A'$ and $\angle BCA$ are corresponding angles)
Therefore, $\vartriangle ABC$ and $\vartriangle A'BC'$ are similar by AA test of similarity.
We know that corresponding sides of similar triangles have the same ratio.
Thus, we get\[\dfrac{{A'B}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{{BC'}}{{BC}}\].
Using (1), we get\[\dfrac{{A'B}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{{BC'}}{{BC}} = \dfrac{3}{4}\].

Note: In such questions, for deciding the number of equidistant points to be made on ray BX, we consider the denominator of the given scale.
For example, in this question, the scale was $\dfrac{3}{4}$. Its denominator is 4. So, we made 4 points ${B_1},{B_2},{B_3},{B_4}$ on ray BX.