Question

Draw a triangle ABC with side BC = 6cm, AB = 5cm and \[\angle ABC={{60}^{\circ }}\]. Then construct a triangle whose sides are ${{\dfrac{3}{4}}^{th}}$ of the corresponding sides of the triangle ABC.

Answer 1

Hint: In this question, we are given an angle and two sides of a triangle. Firstly, we have to draw a proper triangle using given measurements and then we have to construct another triangle whose sides are ${{\dfrac{3}{4}}^{th}}$ of corresponding sides of the previous triangle. For this, we will use a ruler, protractor and compass. We will first draw one triangle and use it to find another triangle. We will write all steps of construction.

Complete step by step answer:
Let us draw a triangle ABC with sides BC = 6cm, AB = 5cm and \[\angle ABC={{60}^{\circ }}\].
Following are the steps of construction to draw it.
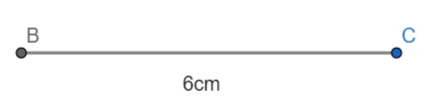
(1): Firstly, let us draw a line segment BC of length 6cm using a ruler.

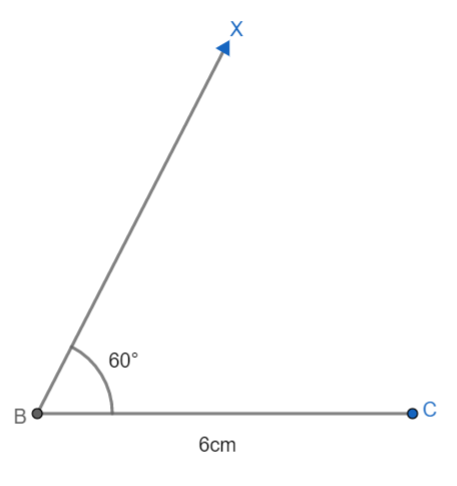
(2): Now with B as center, let us draw an angle of ${{60}^{\circ }}$ such that $\angle XBC={{60}^{\circ }}$ we get,

(3): Now with B as center and 5cm as radius on the compass, let us draw arc on the ray BX which cuts the ray BX at point A. Join A to C, we get,

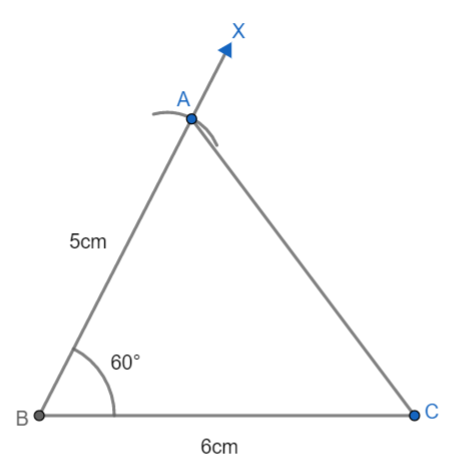
Hence $\Delta ABC$ is our required triangle.
Now let us make a triangle which is ${{\dfrac{3}{4}}^{th}}$ times the size of $\Delta ABC$. For this, following are the steps of construction.
(1): From B, let us draw any ray BX which makes same acute with side BC on the opposite to vertex A. Then let us mark 4 points ${{B}_{1}},{{B}_{2}},{{B}_{3}},{{B}_{4}}$ on BX such that $B{{B}_{1}}={{B}_{1}}{{B}_{2}}={{B}_{2}}{{B}_{3}}={{B}_{3}}{{B}_{4}}$. For this, we shall keep the radius of the compass equal and draw the arcs.

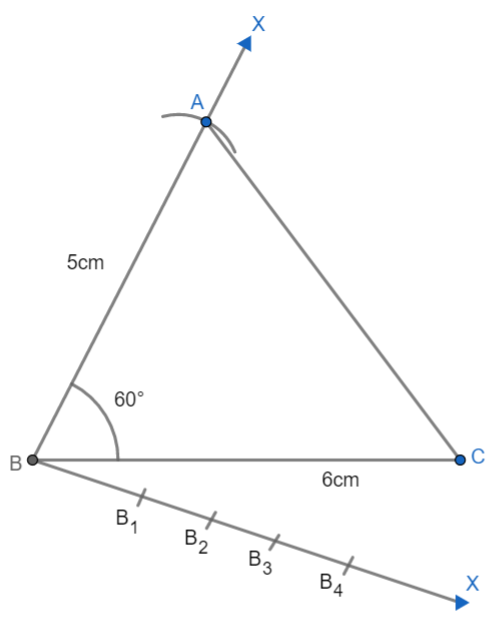
(1): Let us join ${{B}_{4}}$ to C. Now, let us draw a line from ${{B}_{3}}$ to BC which is parallel to ${{B}_{4}}C$. For this, open a compass to some radius and mark angle $B{{B}_{4}}C$. Keeping the same radius draws an arc from ${{B}_{3}}$ which cut the line BX at some point. Then use that point at the center with radius equal to the arc on ${{B}_{4}}$ to draw an arc on the previous arc. Joining this point with ${{B}_{3}}$ and extending will give us a line parallel to ${{B}_{4}}C$ we get:

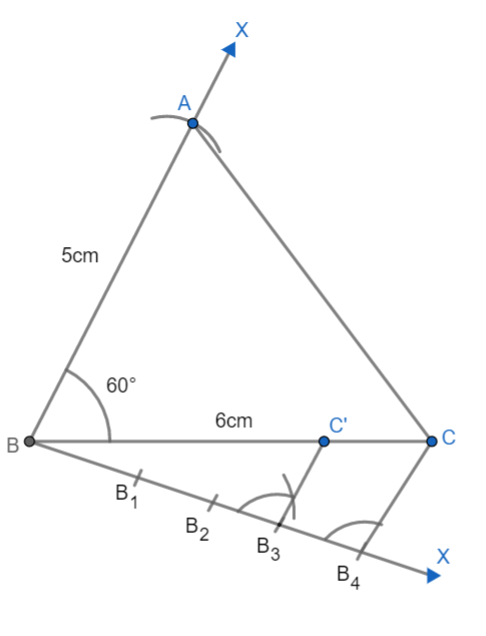
(3): Now similarly, draw a line parallel to AC from C' to the line AB we get:

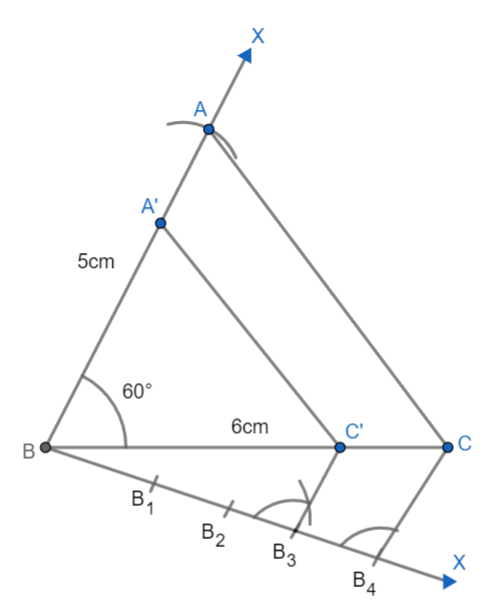
The triangle A'C'B is our required new triangle.

Note: Students should know how to draw parallel lines, angles using compass and ruler only as they are basics for these constructions. Make sure that, pencil is sharp and the compass is tight. Draw all arcs carefully.