Question

Draw an equilateral triangle. Draw its altitudes, medians and angle bisectors. Explain your observation.

Answer 1

Hint:
Draw the above-mentioned diagrams step-by-step one by one.
After all the figures, we have to write the observations made during the drawing of the figures.

Complete step by step solution:
First, we will draw a triangle whose lengths of sides are the same.

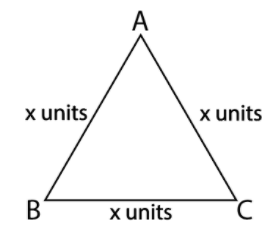
Now, we will draw lines from the vertices A, B and C to the lines BC, AC and AB respectively such that they make 90 degrees on the lines AB, BC and AC. This will give us altitudes.

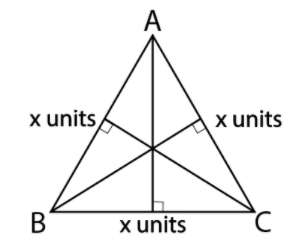
Then, we will draw lines from the vertices A, B and C to the lines BC, AC and AB respectively such that they divide the lines AB, BC and AC in two equal parts. This will give us medians.

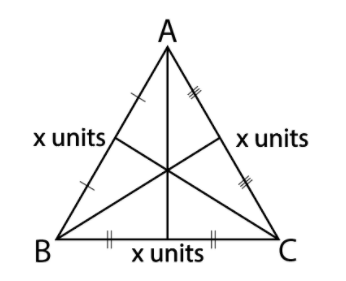
Finally, we will draw lines from the vertices A, B and C to the lines BC, AC and AB respectively such that they divide the angle ABC, angle BCA and angle CAB in two equal parts. This will give us Angle bisectors.

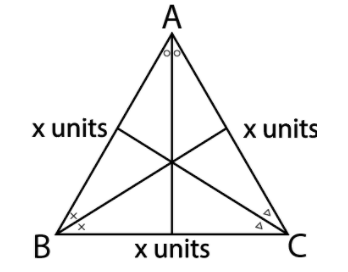
Thus, we observe from the above figures that the orthocentre O, centroid G and in-centre I all lie in the same equilateral triangle.

Note:
Orthocentre: The point where all the three altitudes of a triangle intersect each other is called an orthocentre of that triangle. It is denoted by O.
Centroid: The point where all the three medians of a triangle intersect each other is called a centroid of that triangle. It is denoted by G.
In-centre: The point where the centre of the triangle in-circle, which is the largest circle that can fit into the triangle, lies is called in-centre of that triangle. It is denoted by I.