Question

How do you draw an equilateral triangle without a compass?

Answer 1

Hint: We recall the definition and shape of equilateral triangle. We draw equilateral triangles without a compass using calibrated scale with measurements and a protractor. We first draw one side $BC$ and we draw angle $\angle CBX={{60}^{\circ }},\angle BCY={{60}^{\circ }}$. We denote the point of intersection of $\overrightarrow{BX},\overrightarrow{CY}$ as A.

Complete step by step answer:
A triangle is a polygon with three sides and three vertices otherwise known 3-gon. If we denote the vertices of any triangle as A, B, C then its sides are denote as $\overline{AB},\overline{BC},\overline{AC}$ and length of the sides are denoted as $AB,BC,AC$. If lengths of all sides of a triangle are equal we call the triangle equilateral. If $\Delta ABC$ is an equilateral triangle then we have;
\[AB=BC=AC\]
We also know that the interior angles of the equilateral triangle is ${{60}^{\circ }}$. So we have
\[\angle ABC=\angle ACB=\angle BAC={{60}^{\circ }}\]
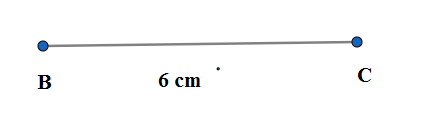
If we want to draw equilateral triangles without a compass we need a calibrated scale and protractor. We draw the one side say $BC=6$ cm with a scale.
 

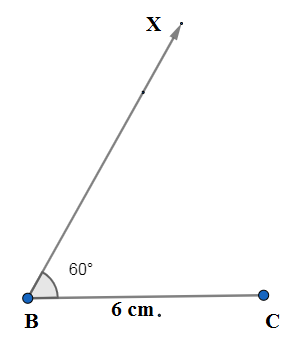
We draw $\angle CBX={{60}^{\circ }}$ with a protractor.

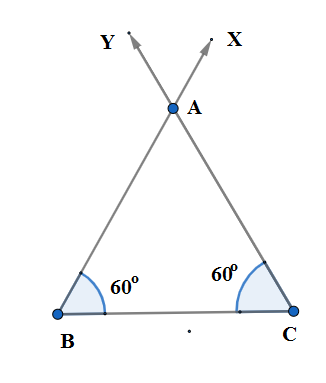
We draw $\angle BCY={{60}^{\circ }}$ with the protractor and denote the point of intersection as $A$.

Note:
We can measure the lengths of the sides $AB=AC=6$cm to verify our construction. We can also construct using the perpendicular bisector of $BC$. We should try to use compasses for accurate construction. If lengths of any two sides are equal we call the triangle isosceles triangle which means one of $AB=BC,BC=AC,AB=AC$ in triangle ABC is true. If the lengths of the triangle are not equal to each other which means $AB\ne BC\ne AC$ then it is called a scalene triangle.