Question

Draw $\angle ABC$ of measure ${{115}^{\circ }}$ and bisect it.

Answer 1

Hint: In order to solve this problem, we have to use a protractor, a compass and ruler. We need to draw the angle first following, draw the angle bisector of it with the help of a compass. It will be helpful if we roughly draw the rough or draw a non-scale draft first.

Complete step-by-step answer:
We need to draw an angle of ${{115}^{\circ }}$ first.
As we can see that ${{115}^{\circ }}$ is greater than ${{90}^{\circ }}$ , so it's an obtuse angle.
An obtuse angle is an angle which is greater than ${{90}^{\circ }}$ .
To get the insight we will draw a rough figure of how the end construction will look like.
So the rough figure is as follows,

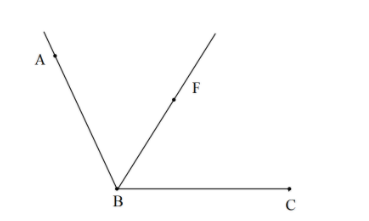
Let's start with drawing the angle first.
For that, first, draw the segment BC.

Also, we need to keep some space upwards so that our angle fits in that space.
Then keeping the middle of the protractor draw ${{115}^{\circ }}$.
We will demonstrate it as follows,

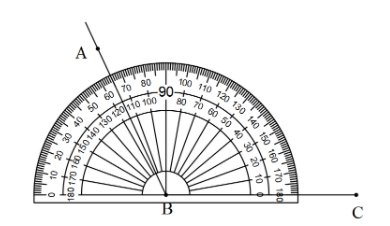
Also, we have to name the segment as AB.
So, the figure now looks like this.

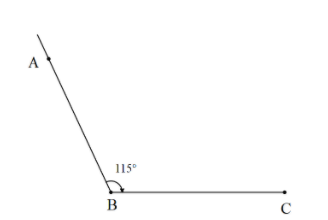
Now, we need to bisect this angle.
Take an approximate distance in the compass usually less than half of the segment and draw the arc cutting AB and BC.
The figure will get is as follows,

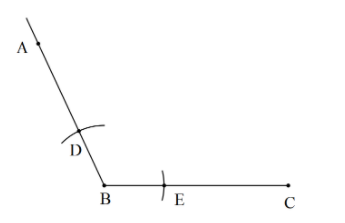
Now, keeping the compass on D take the distance approximately more than half of segment BC and draw the arc in the region between the angle.
And similarly keeping the compass on E take the distance approximately more than half of segment BC and draw the arc in the region between the angle.
We need to keep in mind that arcs from both the points D and E must intersect at a single point.
Now the diagrams look like the following,

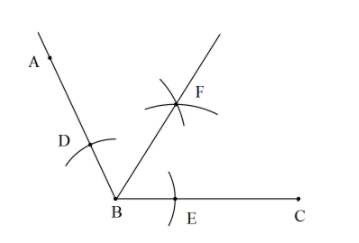
Now we are almost done. We need to join the segment BF.
Therefore, BF is the angle bisector of $\angle ABC$ .


Note: The common mistake of error in this question is we need to use a protractor properly. The counting of zero degrees has to begin from the side of BC and not on the opposite side, otherwise, the angle we will get will be acute. Also, we need to keep in mind that the distance in the compass has to be the same every time or this may lead to a major error. We can also check the angle in the protractor after it's done. Therefore, the $\angle CBF$is half of ${{115}^{\circ }}$ which is ${{57.5}^{\circ }}$ .