Question

Draw $\overline {PQ} $ where PQ = 10cm. Draw circle $ \odot $ (P, 4) and $ \odot $ (Q, 3)
Draw a tangent to each circle from the Centre of the other circle. Write points of construction.

Answer 1

Hint: In this question, first we will draw a line segment PQ of 10cm. After this we will draw two circles, one of radius 4cm and p as the centre and other of 3cm taking Q as the centre. Then we draw the perpendicular bisector of PQ to get midpoint M. Taking M as centre radius equal to MP, we will draw a circle which intersects each of the two circles.

Complete step-by-step answer:
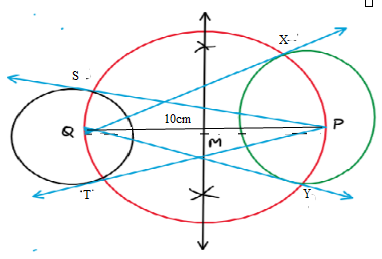
We have given that $\overline {PQ} $ such that PQ = 10cm and circle $ \odot $ (P, 4) and $ \odot $ (Q, 3).
To draw tangents to each circle from the Centre of the other circle, we will follow following steps:
Steps of construction:
(i)Draw $\overline {PQ} $ such that PQ = 10cm.

(ii)After this we will draw two circles, one of radius 4cm and P as the centre and other of 3cm taking Q as the centre.

(iii)Then we draw the perpendicular bisector of PQ to get the midpoint M.

(iv)Now, taking M as the centre point and radius equal to MP, we draw a circle. This circle will cut the two circles at (X, Y) and (P, S) respectively.

(v)To get the tangents, we draw the line segment PS and PT and also QX and QY.

(vi)Thus $\overline {OX} $ and $\overline {OY} $are the tangents from Q to $ \odot \left( {P,4} \right)$ and $\overline {PS} $ are the tangents from P to $ \odot \left( {Q,3} \right)$.

Note: This problem is of construction and this type of problem we need to pay more attention to as little error can cost the whole problem. Meanwhile follow the steps and aso carefully construct the diagram according to the given data. You should know the meaning of the notation $ \odot $ (P, 4), it means that we have to draw a circle of radius 4 cm taking point P as centre.