
Draw the graph of
Answer
488.4k+ views
Hint: For answering this question we need to draw a graph for the function
Complete step-by-step answer:
Now considering from the question we need to draw the graph for the function of
From the basic definition of logarithm of a value for a function
The graph will be continuous and smooth.
The curve is increasing for
The curve of
The logarithm function is of one-one type.
The logarithm function is the inverse of the exponential function.
Properties:
(i)
(ii)
(iii)
(iv)
(v)
Common logarithm has base 10 represented by
Natural logarithm has a base
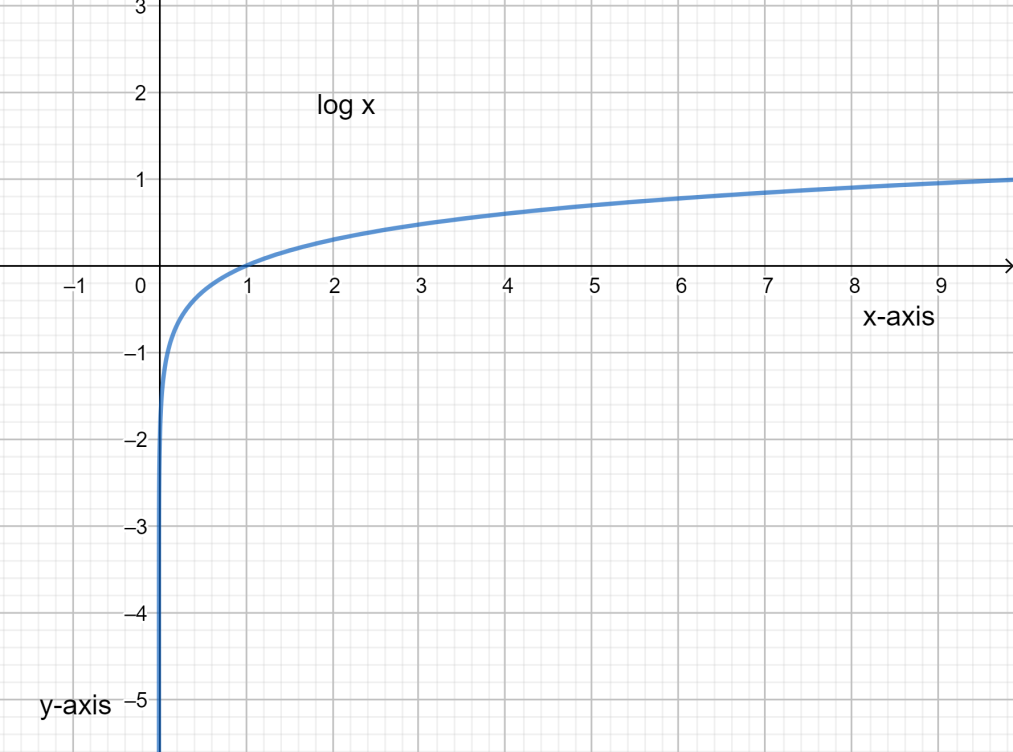
Here we need to draw a graph of common logarithms.
Note: For answering questions based on logarithm functions we use different formulae like
Complete step-by-step answer:
Now considering from the question we need to draw the graph for the function of
From the basic definition of logarithm of a value for a function
The graph will be continuous and smooth.
The curve is increasing for
The curve of
The logarithm function is of one-one type.
The logarithm function is the inverse of the exponential function.
Properties:
(i)
(ii)
(iii)
(iv)
(v)
Common logarithm has base 10 represented by
Natural logarithm has a base
Here we need to draw a graph of common logarithms.

Note: For answering questions based on logarithm functions we use different formulae like
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Discuss the main reasons for poverty in India




