
Answer
437.4k+ views
Hint: Here, we will first substitute different values of \[x\] in the given equation to find different points. We will then draw the graph using the points obtained. Then we will use this graph to get the solution of the equation, for that, we will find the point of intersection of the graph if there is any. The values of the \[x\] coordinate will be the required solution of the given equation.
Complete step-by-step answer:
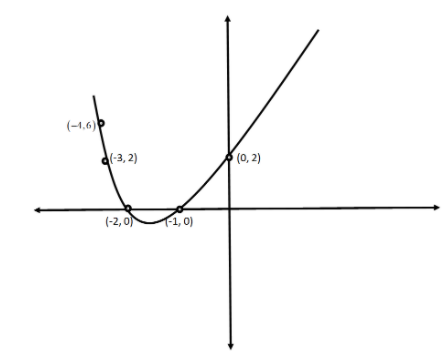
Now, we will first plot the given graph i.e. \[y = {x^2} + 3x + 2\].
We will first draw the table for the graph.
Now, we will plot these points i.e. \[\left( { - 4,6} \right)\], \[\left( { - 3,2} \right)\], \[\left( { - 2,0} \right)\], \[\left( { - 1,0} \right)\], \[\left( {0,2} \right)\], \[\left( {1,6} \right)\], \[\left( {2,12} \right)\] and \[\left( {3,20} \right)\].
Now, we will join the points by a smooth curve. The curve that we have obtained is the graph of
\[y = {x^2} + 3x + 2\].
The given equation is \[{x^2} + 2x + 4 = 0\].
Rewriting the equation, we get
\[ \Rightarrow {x^2} + 3x + 2 - x + 2 = 0\]
We know that \[y = {x^2} + 3x + 2\], therefore, the equation becomes
\[\begin{array}{l} \Rightarrow y - x + 2 = 0\\ \Rightarrow y = x - 2\end{array}\]
The roots of the equation \[{x^2} + 2x + 4 = 0\] is obtained from the point of intersection of the equation \[y = {x^2} + 3x + 2\] and \[y = x - 2\].
Now, we will form the table for the line \[y = x - 2\].
Now, we will plot these points here.
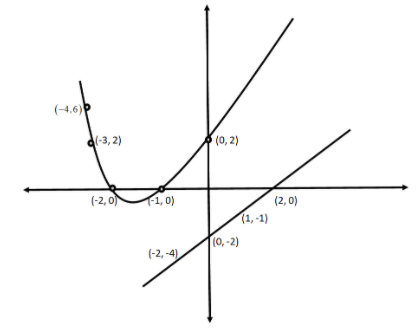
We can see that there is no point of intersection between the straight line and the curve.
Therefore, the equation has no solution.
Note: We know that the number of points of intersection between the straight line and the curve will give us the roots of the given equation. The root of the equation is the solution to the equation. However, we have observed that there is no point of intersection between the straight line and the curve, so there is no solution to the equation. Here, we can take any value of \[x\] and substitute it in the given equation to find the value of \[y\]. So we will get different values of \[y\] for different values of \[x\]. We will use these values as a point \[\left( {x,y} \right)\] and form the graph.
Complete step-by-step answer:
Now, we will first plot the given graph i.e. \[y = {x^2} + 3x + 2\].
We will first draw the table for the graph.
| \[x\] | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 |
| ${{x}^{2}}$ | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| \[3x\] | −12 | −9 | −6 | −3 | 0 | 3 | 6 | 9 |
| \[y\] | 6 | 2 | 0 | 0 | 2 | 6 | 12 | 20 |
Now, we will plot these points i.e. \[\left( { - 4,6} \right)\], \[\left( { - 3,2} \right)\], \[\left( { - 2,0} \right)\], \[\left( { - 1,0} \right)\], \[\left( {0,2} \right)\], \[\left( {1,6} \right)\], \[\left( {2,12} \right)\] and \[\left( {3,20} \right)\].
Now, we will join the points by a smooth curve. The curve that we have obtained is the graph of
\[y = {x^2} + 3x + 2\].

The given equation is \[{x^2} + 2x + 4 = 0\].
Rewriting the equation, we get
\[ \Rightarrow {x^2} + 3x + 2 - x + 2 = 0\]
We know that \[y = {x^2} + 3x + 2\], therefore, the equation becomes
\[\begin{array}{l} \Rightarrow y - x + 2 = 0\\ \Rightarrow y = x - 2\end{array}\]
The roots of the equation \[{x^2} + 2x + 4 = 0\] is obtained from the point of intersection of the equation \[y = {x^2} + 3x + 2\] and \[y = x - 2\].
Now, we will form the table for the line \[y = x - 2\].
| \[x\] | −2 | 0 | 1 | 2 |
| \[y = x - 2\] | −4 | −2 | −1 | 0 |
Now, we will plot these points here.

We can see that there is no point of intersection between the straight line and the curve.
Therefore, the equation has no solution.
Note: We know that the number of points of intersection between the straight line and the curve will give us the roots of the given equation. The root of the equation is the solution to the equation. However, we have observed that there is no point of intersection between the straight line and the curve, so there is no solution to the equation. Here, we can take any value of \[x\] and substitute it in the given equation to find the value of \[y\]. So we will get different values of \[y\] for different values of \[x\]. We will use these values as a point \[\left( {x,y} \right)\] and form the graph.
Recently Updated Pages
Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE




