Question

Draw the graph of $ y=x^3$

Answer 1

Hint: In order to draw the graph for any equation we need to find the local maxima and local minima and where it touches the x-axis and y-axis. Also take some sets of (x,y) by taking x as(-2,-1,0,1,2) to see how a certain graph is going up or down and also find the inflection points.

Complete step-by-step solution:
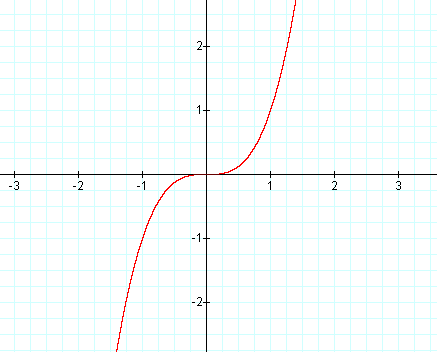
Given that the graph is $ y=x^3$
So let us find the values of local minima and maxima of the function $f(x) = x^3$
We know that for a point to be a local maxima or local minima$f'(x)$ must be zero and $f''$ (x) should not be zero
Which implies $f'$(x)=$\dfrac{d}{{dx}}({x^3}) = 3x^2 = 0$ which implies $x=0$
but $f''$ (x) = $\dfrac{{{d^2}}}{{d{x^2}}}({x^3}) = 6x$ should not be zero which implies x should not be zero
This says that there are no local minima or local maxima for the given function.
From the function $f'$(x) =$\dfrac{d}{{dx}}({x^3}) = 3x^2$ we got to know that derivative of the given fuction is always positive, which implies the given function is always increasing function.
At x=0 we got to know that both $f'(x)$ and $f''(x)$ are zero, which states that x = 0 is an inflection point for the given function .
let us take some sets of the given function
They will be $(-2,-8) , (-1,-1) , (0,0) , (1,1) , (2,8)$
So the graph will be as shown below

Note: Don't just plot a few points and think you have the graph. Find all the things related to a graph which can change the certainty of the graph like inflection points local maxima and local minima and the intervals where the graph will be increasing or decreasing and so on…