Question

Draw the lines of symmetry of the following capital letters of the English alphabet:
(i)A
(ii)D
(iii)T

Answer 1

Hint: We will define symmetry and the line of symmetry. We will identify a line that satisfies the definition for each of the capital letters. Then we will draw the letters with the line of symmetry.

Complete step-by-step answer:
We know that something can be called symmetrical when it is the same on both sides. We know that a shape is said to have symmetry if a central dividing line can be drawn on it, to show that both sides of the shape are exactly the same. This line is called the line of symmetry or the axis of symmetry.
We know that the line of symmetry is imaginary and that it must pass through the centre of the shape or object and divide it into 2 identical halves.
If we fold an image along its line of symmetry, both halves will overlap perfectly.
(i)We will find the line of symmetry of A :

We can see that A has a vertical line of symmetry. The portions to the left and right of the line of symmetry are identical.

(ii)We will find the line of symmetry of D :

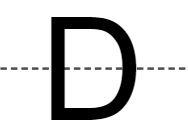
We can see that D has a horizontal line of symmetry. The portions on the upper and lower sides of the line of symmetry are identical.

(iii)We will find the line of symmetry of T :

We can see that T has a vertical line of symmetry. The portions to the left and right of the line of symmetry are identical.

Note: We should know that mirror symmetry is also known as bilateral symmetry. It is the symmetry where an object is symmetrical with respect to its reflection. There are many examples of symmetrical figures in nature; for example, a butterfly is symmetrical along its main body axis. Geometrical figures like squares and other regular polygons have multiple lines of symmetry.