Answer
Verified437.4k+ views
Hint: We need to know that the molecular orbital hypothesis doesn't characterize anything about hybridization of orbitals. Molecular orbital hypothesis can be applied on polyatomic particles. In the molecular orbital hypothesis, bonds are restricted to both two particles and atoms. Molecular orbital hypothesis clarifies about the blending of nuclear orbitals while shaping particles. In the atomic orbital hypothesis, resonance does not play any role.
Complete step by step answer:
We need to know that in molecular orbital hypothesis, nuclear orbitals which structure sub-atomic orbitals don't hold their individual trademark nature. In the molecular orbital hypothesis there is an intricate clarification of the paramagnetic character of oxygen. In the sub-atomic orbitals hypothesis, arrangement of the sub-atomic orbitals depends on the LCAO estimation technique, whereby nuclear orbitals comparing the valence shell of two, just participates in the development of sub-atomic orbitals. In molecular orbital hypothesis, all the electrons of the valence shell are spoken to as having participated in the bonding.
The electronic configuration of dioxygen is,
${{{O}}_{{2}}}{{ = }}{\left( {{{{\sigma }}_{{{1s}}}}} \right)^{{2}}}{\left( {{{{\sigma }}^{{*}}}_{{{1s}}}} \right)^{{2}}}{\left( {{{{\sigma }}_{{{2s}}}}} \right)^{{2}}}{\left( {{{{\sigma }}^{{*}}}_{{{2s}}}} \right)^{{2}}}{\left( {{{{\sigma }}_{{{2pz}}}}} \right)^{{2}}}{\left( {{{{\pi }}_{{{2px}}}}} \right)^{{2}}}{{ = }}{\left( {{{{\pi }}_{{{2py}}}}} \right)^{{2}}}{\left( {{{{\pi }}^{{*}}}_{{{2px}}}} \right)^{{1}}}{{ = }}{\left( {{{{\pi }}^{{*}}}_{{{2py}}}} \right)^{{1}}}$
The molecular orbital diagram of ${{{O}}_{{2}}}$ is,
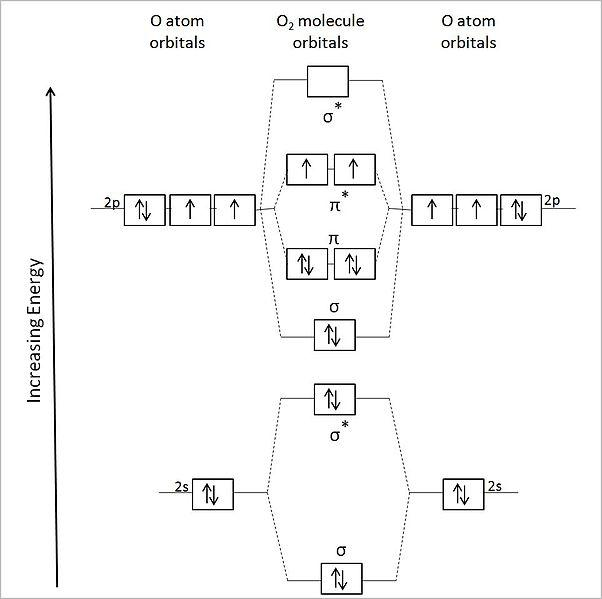
The bond order of ${{{O}}_{{2}}}$ is,
${{B}}{{.O = }}\dfrac{{{{{N}}_{{b}}}{{ - }}{{{N}}_{{a}}}}}{{{2}}}$
Where,
${N_b}$ - Number of bonding electrons
${N_a}$ - Number of antibonding electrons
Now we can substitute the values we get,
${{B}}{{.O = }}\dfrac{{{{10 - 6}}}}{{{2}}}$
On simplification we get,
${{B}}{{.O = 2}}$
The bond order of ${{{O}}_{{2}}}$ is two.
Note: We must need to know that the localized bonding hypothesis characterizes the hybridization of sub-atomic orbitals it must be applied for diatomic particles though In this hypothesis, bonds are limited to two iotas and not atoms. It clarifies about particles involving nuclear orbitals. Here, resonance assumes a significant part In this hypothesis, particles which are associated with the bond arrangement, keep up their individual trademark nature. In the valence bond hypothesis, there is no clarification of paramagnetic character of oxygen. In valence bond hypothesis, the subsequent sub-atomic orbital is acquired by the mix of two wave elements of two unpaired electrons. In the valence bond hypothesis, a portion of the valence electrons are spoken to as not shared and not associated with the arrangement of the atom.
Complete step by step answer:
We need to know that in molecular orbital hypothesis, nuclear orbitals which structure sub-atomic orbitals don't hold their individual trademark nature. In the molecular orbital hypothesis there is an intricate clarification of the paramagnetic character of oxygen. In the sub-atomic orbitals hypothesis, arrangement of the sub-atomic orbitals depends on the LCAO estimation technique, whereby nuclear orbitals comparing the valence shell of two, just participates in the development of sub-atomic orbitals. In molecular orbital hypothesis, all the electrons of the valence shell are spoken to as having participated in the bonding.
The electronic configuration of dioxygen is,
${{{O}}_{{2}}}{{ = }}{\left( {{{{\sigma }}_{{{1s}}}}} \right)^{{2}}}{\left( {{{{\sigma }}^{{*}}}_{{{1s}}}} \right)^{{2}}}{\left( {{{{\sigma }}_{{{2s}}}}} \right)^{{2}}}{\left( {{{{\sigma }}^{{*}}}_{{{2s}}}} \right)^{{2}}}{\left( {{{{\sigma }}_{{{2pz}}}}} \right)^{{2}}}{\left( {{{{\pi }}_{{{2px}}}}} \right)^{{2}}}{{ = }}{\left( {{{{\pi }}_{{{2py}}}}} \right)^{{2}}}{\left( {{{{\pi }}^{{*}}}_{{{2px}}}} \right)^{{1}}}{{ = }}{\left( {{{{\pi }}^{{*}}}_{{{2py}}}} \right)^{{1}}}$
The molecular orbital diagram of ${{{O}}_{{2}}}$ is,
The bond order of ${{{O}}_{{2}}}$ is,
${{B}}{{.O = }}\dfrac{{{{{N}}_{{b}}}{{ - }}{{{N}}_{{a}}}}}{{{2}}}$
Where,
${N_b}$ - Number of bonding electrons
${N_a}$ - Number of antibonding electrons
Now we can substitute the values we get,
${{B}}{{.O = }}\dfrac{{{{10 - 6}}}}{{{2}}}$
On simplification we get,
${{B}}{{.O = 2}}$
The bond order of ${{{O}}_{{2}}}$ is two.
Note: We must need to know that the localized bonding hypothesis characterizes the hybridization of sub-atomic orbitals it must be applied for diatomic particles though In this hypothesis, bonds are limited to two iotas and not atoms. It clarifies about particles involving nuclear orbitals. Here, resonance assumes a significant part In this hypothesis, particles which are associated with the bond arrangement, keep up their individual trademark nature. In the valence bond hypothesis, there is no clarification of paramagnetic character of oxygen. In valence bond hypothesis, the subsequent sub-atomic orbital is acquired by the mix of two wave elements of two unpaired electrons. In the valence bond hypothesis, a portion of the valence electrons are spoken to as not shared and not associated with the arrangement of the atom.