Question

Draw the shape of five d-orbitals.

Answer 1

Hint:. Atomic orbitals:- The three-dimensional space around the atom of an element in which the electron density is maximum. It means the probability of finding an electron is maximum.


Complete step by step answer:
The transition metal ions of the outermost d-orbitals are not completely filled with electrons and hence, they can easily take and give electrons.
For d-orbitals the value of l = $2$ , so, the value of m will be: $-lto+l.(-2,-1,0,+1,+2)$.
As we see that there are five magnetic quantum numbers, so, the d-orbital will have five orientations. It means, five types of shapes of d-orbital in three-dimensional space.
So, depending upon the axes along which or between which the electron clouds are obtained, different names and shapes are given as;
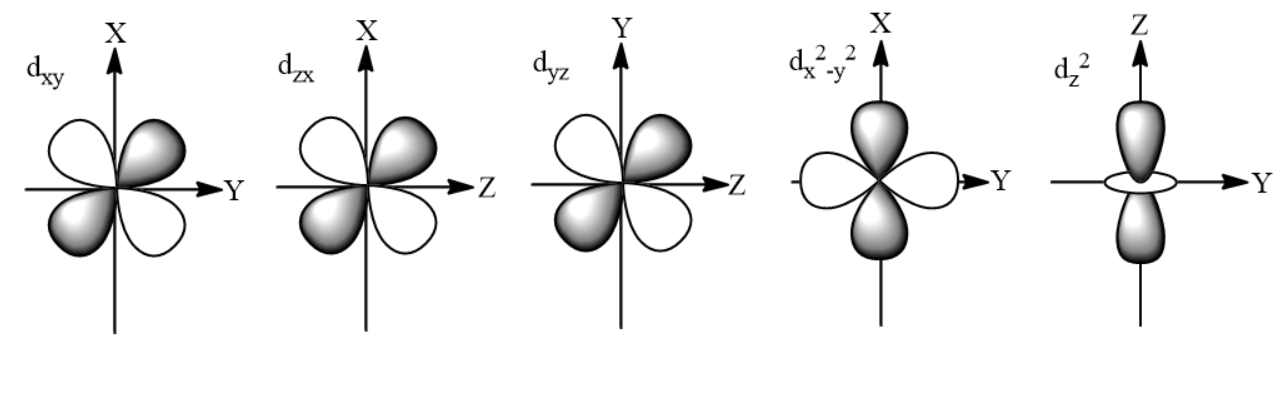
$d_{xy}$ = It is of cloverleaf-like shape.
$d_{yz}$ = It is of cloverleaf-like shape.
$d_{xz}$ = It is of cloverleaf-like shape.
${d_{x^2}}_{-y^2}$ =It is of cloverleaf-like shape.
$d_{z^2}$ = It is of ‘dumbbell’ and ‘doughnut’ like shape. The lobes of the ‘dumbbell' lie along the z-axis and ‘doughnut’ lies in the xy plane.
It is clear from the above names of the five d-orbitals that in which position will be assigned to them in the xyz coordinates, so the shapes are:

Additional Information:
Significance of four quantum numbers:
The principal quantum number $n$ = It describes the energy and distance from the nucleus and represents the shell.
The azimuthal quantum number $l$ = It describes the shape of the subshell and its orbitals.
The magnetic quantum number $m$ = It describes the orientation of the orbitals in space.
The spin quantum number $s$ = It describes the spin of each electron in the orbital.

Note: The possibility to make a mistake is that ${d_{x^2}}_{-y^2}$ has a cloverleaf-like shape and not dumbbell as the lobes are present in the $xy$ plane only.