Question

Each angle of a Rectangle is a right angle.
State whether the above statement is true or false.
(A) True
(B) False

Answer 1

Hint: In this question we are asked about the property of a rectangle that is if each angle of a rectangle is a right angle or not. For approaching such kinds of questions, we need to first keep in mind the definition and properties of quadrilaterals, which tells us that the sum of all internal angles of a quadrilateral is \[360\] degrees, so we will find the value of each internal angle of the rectangle. And then we will see if each of its angles is right or not.

Complete step by step answer:
We are given a statement that each angle of a rectangle is a right angle, and we are asked if the statement is true or false. So, we know that a rectangle is a quadrilateral in which opposite sides are of equal length, and all the four angles are equal.
Now, let us consider a rectangle \[ABCD\] ,as shown in the figure below.

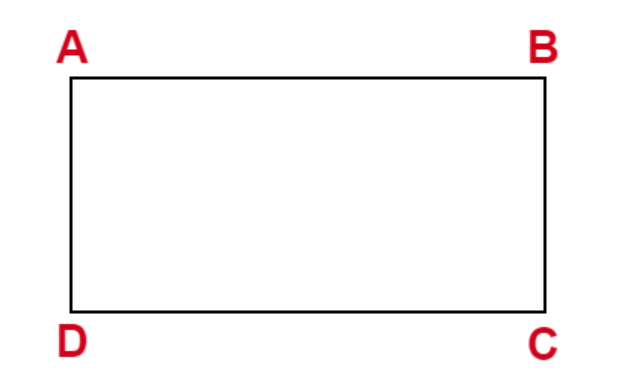
As per the definition of rectangle, we have \[AB = CD\] and \[AD = BC\]
And \[\angle \left( {ABC} \right) = \angle \left( {BCD} \right) = \angle \left( {CDA} \right) = \angle \left( {DAB} \right)\]
But we know that \[ABCD\] is a quadrilateral and the sum of all interior angles of a quadrilateral is \[360\] degrees. Thus, we have,
\[\angle \left( {ABC} \right) + \angle \left( {BCD} \right) + \angle \left( {CDA} \right) + \angle \left( {DAB} \right) = {360^ \circ }\]
Hence, we can write
\[\angle \left( {ABC} \right) = \angle \left( {BCD} \right) = \angle \left( {CDA} \right) = \angle \left( {DAB} \right) = \dfrac{{{{360}^ \circ }}}{4} = {90^ \circ }\]
Thus, we now know that all four angles of a rectangle are equal to \[{90^ \circ }\] degrees, or a right angle.
Hence, the given statement that each angle of a rectangle is a right angle is true. So, the correct answer is option (A).

Note:
A quadrilateral is a polygon that has four sides. The diagonal of a quadrilateral divides it into two triangles, as we know the sum of all interior angles of a triangle is \[180\] degrees, the sum of all interior angles of a quadrilateral is \[360\] degrees. As the rectangle also has \[4\] sides, it is a type of quadrilateral and thus follows the quadrilateral angle sum property. That’s why the sum of all the angles in a rectangle is equal to \[360\] degrees.