Question

Each rectangle is $6$ cm long and $3$ cm wide; they share a common diagonal of PQ. How do you show that $\tan \alpha =\dfrac{3}{4}$?

Answer 1

Hint: Here we have to find the value of $\alpha $ , where we will follow the rule of congruence of triangle. By which we get two triangles that are congruent. After that we will find the ratio of sides that would be equal because both the triangles are congruent. From the above step, we can see that the lines are equal also. So, we will use them to get the value of $\alpha $ .

Complete step-by-step answer:
First of all we will name the diagram so that it will be easy to proceed further.
So, the diagram will be as:

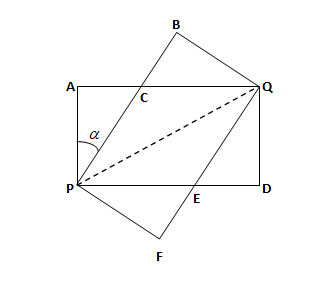
From the diagram, we can see that the value of $\alpha $:
$\Rightarrow \text{Tan}\alpha =\dfrac{AC}{AP}$ … $\left( i \right)$
Since, we have some values from the question that are:
$\Rightarrow AP=QD=PF=BQ=3$ cm
And
$\Rightarrow AQ=PD=PB=FQ=6$ cm
So, the equation $\left( i \right)$ will be as:
$\Rightarrow \text{Tan}\alpha =\dfrac{AC}{3}$ … $\left( ii \right)$
For value of $AC$, we will follow the below procedure as:
Here, from the diagram we can say that the triangle $\Delta ACP$ and $\Delta BCQ$ are congruent on the basis of Right Angle-Hypotenuse-Side rule so that we can write it as:
$\Rightarrow \Delta ACP\cong \Delta BCQ$
Since, we know that the triangle $\Delta ACP$ and $\Delta BCQ$ is congruent. So, the sides are equal as:
$\Rightarrow AC=BC$
And
$\Rightarrow CP=CQ$
Since, $\Delta ACP$ is a right angle triangle, we will use Pythagoras Principle as:
$\Rightarrow P{{C}^{2}}=A{{P}^{2}}+A{{C}^{2}}$ … $\left( iii \right)$
Since, we can see from the diagram that:
$\Rightarrow AQ=AC+CQ$
Since, It is given that $AQ=6$, the above equation will be as:
$\Rightarrow 6=AC+CQ$
We can get the value of $CQ$ in the term of $AC$ as:
$\Rightarrow CQ=6-AC$
Since, we know that $CP=CQ$ from the congruent rule. So, the above equation will be as:
$\Rightarrow PC=6-AC$
Now, put the value of $PC$ in the equation $\left( iii \right)$. So we will get the equation $\left( iii \right)$ as:
$\Rightarrow {{\left( 6-AC \right)}^{2}}=A{{P}^{2}}+A{{C}^{2}}$
Here, we will open the bracket by using formula ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ , the above equation will as:
$\Rightarrow {{6}^{2}}+A{{C}^{2}}-2\times 6\times AC=A{{P}^{2}}+A{{C}^{2}}$
Here, $A{{C}^{2}}$ will be cancel out and the above equation can be written as:
$\Rightarrow {{6}^{2}}-12AC=A{{P}^{2}}$
Since, we have $AP=3$, then the above equation would be:
$\Rightarrow {{6}^{2}}-12AC={{3}^{2}}$
Now, we will do the required calculation:
$\Rightarrow 36-12AC=9$
$\Rightarrow 36-9=12AC$
Here, we chance the place of equation as:
$\Rightarrow 12AC=36-9$
$\Rightarrow 12AC=27$
$\Rightarrow AC=\dfrac{27}{12}$
$\Rightarrow AC=\dfrac{9}{4}$
Since, we got the value of $AC$ , we will apply it in equation $\left( ii \right)$
$\Rightarrow \text{Tan}\alpha =\dfrac{\dfrac{9}{4}}{3}$
The above equation can be written as:
$\Rightarrow \text{Tan}\alpha =\dfrac{9}{4}\times \dfrac{1}{3}$
$\Rightarrow \text{Tan}\alpha =\dfrac{3}{4}$
Hence, we had the value of $\alpha $ as $\text{Tan}\alpha =\dfrac{3}{4}$ .

Note: Here, we will check that the solution is correct or not in the following way:
Since, we have the value of $\alpha $for the triangle $\Delta ACP$ from the solution that is:
$\Rightarrow \text{Tan}\alpha =\dfrac{3}{4}$ … $\left( 1 \right)$
In the triangle $\Delta ACP$ , we know that:
$\Rightarrow \text{Tan}\alpha =\dfrac{AC}{AP}$ … $\left( 2 \right)$
From the equation $\left( 1 \right)$ and $\left( 2 \right)$ , we have:
$\Rightarrow \dfrac{AC}{AP}=\dfrac{3}{4}$ … $\left( 3 \right)$
This implies that –
$\Rightarrow AC=3$
And
$\Rightarrow AP=4$
But given that
$\Rightarrow AP=3$
That means the above value is wrong. So we will multiply by $\dfrac{3}{3}$ in equation $\left( 3 \right)$ :
$\Rightarrow \dfrac{AC}{AP}=\dfrac{3}{4}\times \dfrac{3}{3}$
We can write the above equation as:
$\Rightarrow \dfrac{AC}{AP}=\dfrac{\dfrac{3}{4}\times 3}{3}$
$\Rightarrow \dfrac{AC}{AP}=\dfrac{\dfrac{9}{4}}{3}$
Now, we have the correct values as:
$\Rightarrow AC=\dfrac{9}{4}$
And
$\Rightarrow AP=3$