
What is the eccentric angle in the first quadrant of a point on the ellipse
(A).
(B).
(C).
(D).
Answer
522k+ views
Hint- In such types of questions, just follow the simple approach first take the parametric equation of ellipse
Complete step-by-step solution -
Let us suppose the point
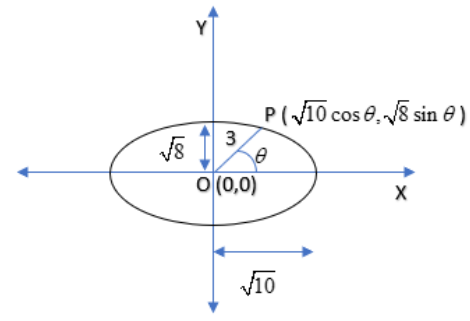
Now we have
We have the parametric equation of the ellipse as
Now, we know that the distance formula to calculate distance between two points say A
Here the two points are
So,
Now, d = 3 as given in the question so we get,
Squaring both sides, we get,
Now we know that
We know that
So, we have
Hence, the eccentric angle in the first quadrant of a point on the ellipse
Note- In such types of questions, just keep in mind the distance formula to calculate the distance between two points i.e. for two points say two points say A
Complete step-by-step solution -
Let us suppose the point

Now we have
We have the parametric equation of the ellipse as
Now, we know that the distance formula to calculate distance between two points say A
Here the two points are
So,
Now, d = 3 as given in the question so we get,
Squaring both sides, we get,
Now we know that
We know that
So, we have
Hence, the eccentric angle in the first quadrant of a point on the ellipse
Note- In such types of questions, just keep in mind the distance formula to calculate the distance between two points i.e. for two points say two points say A
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




