Question

EFGH is a parallelogram. EI bisects angle E and GJ bisects angle G. I lie on GH and J lies on EF. Show that EI is parallel GJ and EJGI is a parallelogram.

Answer 1

Hint: First we will draw the diagram according to the given information. Then, we will use the properties of the parallelogram. Here, we will prove that EI || GJ and IG || EJ. As we know, a parallelogram is a quadrilateral with two pairs of parallel sides. Thus, according to this, EJGI is a parallelogram and hence, we have proved the final output.

Complete step-by-step answer:
EFGH is a parallelogram.
According to the given information, we can draw the figure as below:

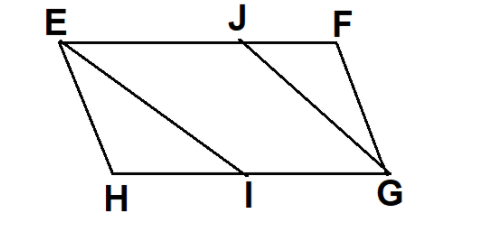
According to the property of the parallelogram,
1) Opposite angles are equal:
 \[\angle E = \angle G\] and \[\angle F = \angle H\]
2) Sum of the adjacent angles is equal to 180 degree:
 \[\angle E + \angle F = {180^\circ }\] (i.e. angle E and angle F are supplementary angles)
 \[\angle G + \angle H = {180^\circ }\] (i.e. angle G and angle H are supplementary angles)
Since given that,
EI bisects \[\angle E\]
 \[ \Rightarrow \angle FEH = \angle E\]
 \[ \Rightarrow \angle FEI = \angle IEH = \dfrac{{\angle E}}{2}\]
 \[\therefore \angle JEI = \dfrac{{\angle E}}{2}\]
Also, given that,
GJ bisects \[\angle G\]
 \[ \Rightarrow \angle FGH = \angle G\]
 \[ \Rightarrow \angle FGJ = \angle JGH = \dfrac{{\angle G}}{2}\]
 \[\therefore \angle JGI = \dfrac{{\angle G}}{2}\]
We know that, exterior angle of a triangle is equal to the sum of opposite interior angles.
 \[\therefore \angle EJG = \angle JGF + \angle F\]
 \[ \Rightarrow \angle EJG = \dfrac{{\angle G}}{2} + \angle F\] \[(\because \angle JGF = \dfrac{{\angle G}}{2})\]
 \[ \Rightarrow \angle EJG = \dfrac{{\angle E}}{2} + \angle F\] \[\left( {\because \angle E = \angle G} \right)\]
Now adding,
 \[\angle JEI\; + \angle EJG\]
 \[ = \dfrac{{\angle E}}{2}{\text{ + }}\dfrac{{\angle E}}{2} + \angle F\]
 \[ = \dfrac{{2\angle E}}{2} + \angle F\]
 \[ = \angle E + \angle F\]
 \[ = {180^\circ }\]
 \[\therefore \angle JEI\; + \angle EJG{\text{ }}\; = EI||GJ\]
Thus, \[EI||GJ\] is proved.
Next, we need to prove that, EJGI is a parallelogram.
Here, in the quadrilateral EJGI,
EI || GJ (this is proved above)
Since, we know that in a quadrilateral, the parts of parallel lines are also parallel.
Also, GH || EF
 \[\therefore \] IG || EJ
Here, both the pairs of the opposite sides are parallel
 \[\therefore \] EJGI is a parallelogram.

Note: A parallelogram is a type of polygon having four sides. A parallelogram is equal in length to the opposite sides and the opposite angles are equal in measure. Also, they are supplementary angles because these interior angles lie on the same side of the transversal. Sum of all the interior angles equals 360 degrees. A square and a rectangle are two shapes which have similar properties of a parallelogram.