
When an elastic material with Young’s modulus Y is subjected to stretching stress S, elastic energy stored per unit volume of the material is
Answer
497.7k+ views
Hint: When an elastic material is subjected to stretching stress, the work done in stretching it is stored in the form of potential energy in the wire. Let us say we extend the wire of length L, area of cross section A and Young’s modulus Y by
Complete answer:
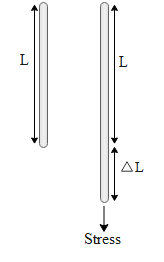
In the above diagram we can see that the wire of length L gets extended to a final length of
Multiplying and dividing by L the above equation we get,
The term
Hence the above equation becomes,
The Young’s modulus for a wire is given by stress (S) by strain i.e.
So, the correct answer is “Option C”.
Note:
The above condition is analogous to potential energy of a spring. As we extend the spring the force required is directly proportional to the length of extension. If we still want to extend it further more and more force is required to extend any further.
Complete answer:
In the above diagram we can see that the wire of length L gets extended to a final length of

Multiplying and dividing by L the above equation we get,
The term
Hence the above equation becomes,
The Young’s modulus for a wire is given by stress (S) by strain i.e.
So, the correct answer is “Option C”.
Note:
The above condition is analogous to potential energy of a spring. As we extend the spring the force required is directly proportional to the length of extension. If we still want to extend it further more and more force is required to extend any further.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




