Question

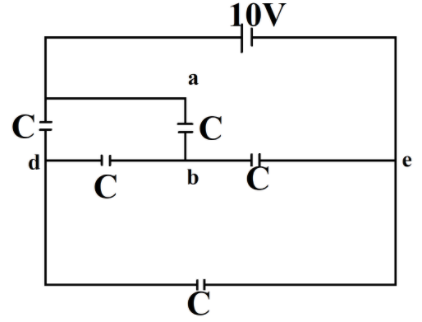
What is the energy stored in the capacitor between the terminals a and b of the network shown in the figure?
Capacitance of each capacitor $C=1\mu F$)

A. $12.5\mu J$
B. Zero
C. $25\mu J$
D. $50\mu J$

Answer 1

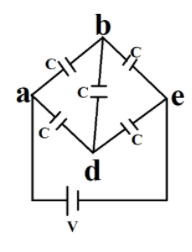
Hint: If you look closely at the diagram, you will notice that there is a wheatstone network in here. It is a balanced Wheatstone network. So, it can easily be solved using the concept of a wheatstone bridge. In a balanced Wheatstone Bridge, It is said that both sides of the parallel bridge network are balanced since the voltage at point C is equal to the voltage at point D, with zero being the difference.
Formula used:
For solving this question, we will be using the formula
Q = CV

Step by step solution:
First, let us redraw the diagram to make it a Wheatstone network
Now, Applying the concept of the balanced Wheatstone bridge,
$C_{eq}=C$
Now, The Charge on capacitor between the terminals a and b

${\displaystyle \frac{Q}{2}}={\displaystyle \frac{CV}{2}}$
Now, for the energy stored in the capacitor between a and b,
$$={\displaystyle \frac{{({\displaystyle \frac{Q}{2}})}^2}{2C}}={\displaystyle \frac{Q^2}{8C}}$$
Now, using
Q = CV
We have
$\begin{array}{rl}& \Rightarrow Q={\displaystyle \frac{C^2{V}^2}{8C}}\\ & \end{array}$
$\Rightarrow Q={\displaystyle \frac{C{V}^2}{8}}$
Now, as
$C=1\mu F$
And, V = 10 V
Takin the given values,
$\begin{array}{rl}& \Rightarrow U={\displaystyle \frac{(1\times {10}^{-6})\times {10}^2}{2C}}\\ & \end{array}$
$\Rightarrow U={\displaystyle \frac{100}{8}}\times {10}^{-6}$
$\Rightarrow U=12.5\mu J$

So, the energy stored in the capacitor between the terminals a and b of the network shown in the figure will be $12.5\mu J$, i.e., Option – A.

Note:
The network (or bridge) of Wheatstone is a circuit for indirect resistance calculation by a null reference approach relative to an established normal resistance. It consists of four R1, R2, R3 and R4 resistors connected to a quadrilateral ABCD. The Wheatstone bridge was created by the British Scientist, mathematician and physicist, Samuel Hunter Christie in 1843.