Question

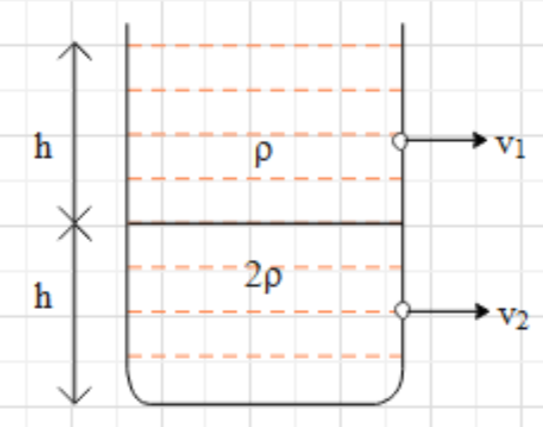
Equal volume of two immiscible liquids of densities $\rho $ and $2\rho $ are filled in a vessel as shown in the figure. Two small holes are made at depth $\dfrac{h}{2}$ and $\dfrac{3h}{2}$ from the surface of the lighter liquid. If ${{v}_{1}}$ and ${{v}_{2}}$ are the velocities of efflux at these two holes, then $\dfrac{{{v}_{1}}}{{{v}_{2}}}$ will be

$\text{A}\text{. }\dfrac{1}{\sqrt{2}}$
$\text{B}\text{. }\dfrac{1}{2\sqrt{2}}$
$\text{C}\text{. }\dfrac{1}{2}$
$\text{D}\text{. }\dfrac{1}{2}$

Answer 1

Hint: Use Bernoulli’s theorem to find the two velocities of efflux. The Bernoulli’s theorem for two points A and B is given as ${{\rho }_{A}}g{{h}_{A}}+\dfrac{1}{2}{{\rho }_{A}}v_{A}^{2}={{\rho }_{B}}g{{h}_{B}}+\dfrac{1}{2}{{\rho }_{B}}v_{B}^{2}$, where the pressures at A and B are ${{\rho }_{A}}$ and ${{\rho }_{B}}$, depths of A and B are ${{h}_{A}}$ and ${{h}_{B}}$. ${{v}_{A}}$ and ${{v}_{B}}$ are the velocities of the liquid at the points A and B respectively.
Formula used:
${{\rho }_{A}}g{{h}_{A}}+\dfrac{1}{2}{{\rho }_{A}}v_{A}^{2}={{\rho }_{B}}g{{h}_{B}}+\dfrac{1}{2}{{\rho }_{B}}v_{B}^{2}$

Complete step-by-step solution:
In the given case, there is a container in which two immiscible liquids are present. Since the two liquids are immiscible, they will not interact and mix with each other. Hence, the liquid, which has the least density will be at the top and the liquid with higher density will set down. It is given that the heights of both the liquid layers are equal to h.

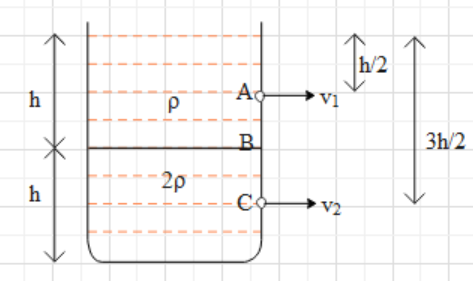
Now, we punch two holes in the container. One hole at a depth of $\dfrac{h}{2}$ and the other at $\dfrac{3h}{2}$, both from the surface of the top liquid (as shown). Due to these holes, the liquids come with velocities ${{v}_{1}}$ and ${{v}_{2}}$.
Therefore, there is a flow of both the liquids. When there is a flow of liquid, Bernoulli's theorem comes into role.
Let us apply Bernoulli's theorem, at the points A and B.
Hence, we get,
$\rho g\left( \dfrac{h}{2} \right)+\dfrac{1}{2}\rho v_{1}^{2}=\rho gh+0$
$\Rightarrow \dfrac{1}{2}v_{1}^{2}=g\left( \dfrac{h}{2} \right)$
$\Rightarrow v_{1}^{2}=gh$
$\Rightarrow {{v}_{1}}=\sqrt{gh}$.
Therefore, the speed of the liquid coming out from point A is ${{v}_{1}}=\sqrt{gh}$.
Now, apply the Bernoulli’s theorem at points B and C.
  $\rho gh+0=(2\rho )g\left( \dfrac{3h}{2} \right)+\dfrac{1}{2}(2\rho )v_{2}^{2}$
$\Rightarrow gh=2g\left( \dfrac{3h}{2} \right)+v_{2}^{2}$
$\Rightarrow v_{2}^{2}=2gh$
$\Rightarrow {{v}_{2}}=\sqrt{2gh}$.
Therefore, the speed of the liquid coming out from point C is ${{v}_{2}}=\sqrt{2gh}$.
Therefore, $\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{\sqrt{gh}}{\sqrt{2gh}}=\dfrac{1}{\sqrt{2}}$

Hence, the correct option is A.

Note: When a liquid comes out of holes made in the container, the velocity of the liquid is called the velocity of efflux and is given as $v=\sqrt{2gH}$,
Where H is the depth of the hole from the top surface where the liquid is in contact with air.
Therefore, ${{v}_{1}}=\sqrt{2g\left( \dfrac{h}{2} \right)}=\sqrt{gh}$.
Then we can find ${{v}_{2}}$ by applying Bernoulli’s theorem at points A and C.