
What is the equation of the perpendicular bisector of a chord of a circle?
Answer
443.7k+ views
Hint: Here in this question we have been asked for the equation of the perpendicular bisector of a chord of a circle for answering this question we will assume two end points of a chord of a circle and find its midpoint through which the perpendicular bisector will pass.
Complete step-by-step answer:
Now considering from the question we have been asked for the equation of the perpendicular bisector of a chord of a circle.
Let us assume a chord
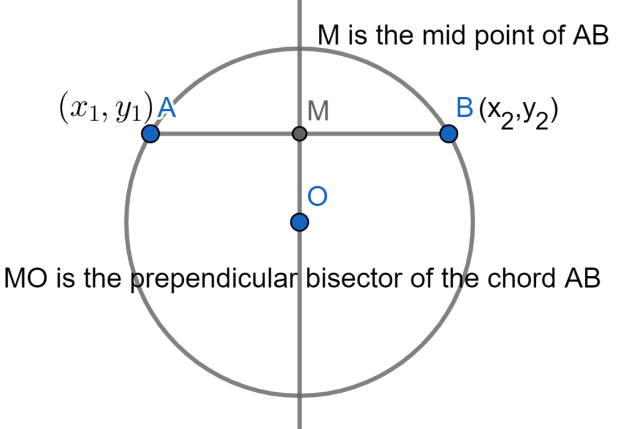
From the basic concepts we know that the midpoint of the line formed by the points
The midpoint of the chord
From the basic concepts we know that the slope of the line formed by the points
The slope of the chord
From the basic concepts we know that the product of slopes of two perpendicular lines will be given as
Now we can say that the perpendicular of the chord will pass through the midpoint and has the slope
From the basic concepts we know that the line of an equation passing through a point
Hence we can say that the equation of perpendicular bisector will be given as
Therefore we can conclude that the equation of the perpendicular bisector of a chord of a circle will be given as
Note: In the process of answering questions of this type we should be sure with the concepts that we are going to apply in between the steps. Someone can make mistakes if they have some confusion in the concept.
Complete step-by-step answer:
Now considering from the question we have been asked for the equation of the perpendicular bisector of a chord of a circle.
Let us assume a chord

From the basic concepts we know that the midpoint of the line formed by the points
The midpoint of the chord
From the basic concepts we know that the slope of the line formed by the points
The slope of the chord
From the basic concepts we know that the product of slopes of two perpendicular lines will be given as
Now we can say that the perpendicular of the chord will pass through the midpoint and has the slope
From the basic concepts we know that the line of an equation passing through a point
Hence we can say that the equation of perpendicular bisector will be given as
Therefore we can conclude that the equation of the perpendicular bisector of a chord of a circle will be given as
Note: In the process of answering questions of this type we should be sure with the concepts that we are going to apply in between the steps. Someone can make mistakes if they have some confusion in the concept.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




